Extrempunkte berechnen - Hochpunkt und Tiefpunkt Rechner
Extrempunkt Rechner
Der Online Rechner von Simplexy kann dir bei der Extrempunkt Berechnung sehr helfen. Mit dem Rechner kannst du dir den Graphen einer Funktion zeichnen lassen, die Funktion ableiten und viel mehr.
Extrempunkte berechnen
Hochpunkt und Tiefpunkt berechnen
In dem folgenden Video ist die Berechung der Extrempunkte für eine Funktion durchgeführt.
Damit eine Funktion Extremstellen besitzt, muss sowohl die notwendige als auch die hinreichende Bedingung für die Existenz von Extremstellen erfüllt sein.
1. Notwendige Bedingung:
\(f'(x_E)=0\)
\(\implies\)
potentielle Extremstelle bei \(x_E\)
Ist die erste Ableitung einer Funktion an der Stelle \(x_E\) gleich Null, dann wissen wir, dass sich dort ein potentieller Extrempunkt befindet. Ein potentieller Extrempunkt ist nicht sofort ein Hochpunkt oder ein Tiefpunkt. Es kann sich dabei auch um einen Sattelpunkt handeln. Um sicher zu gehen, dass es sich tatsächlich um einen Extrempunkt handelt, muss die hinreichende Bedingung erfüllt sein.
2. Hinreichende Bedingung:
\(f'(x_E)=0\) und \(f''(x_E)\ne 0\)
\(\implies\)
Extremstelle bei \(x_E\).
Ist die erste Ableitung einer Funktion an einer potentiellen Extremstelle \(x_E\) null und die zweite Ableitung der Funktion an dieser potentiellen Extremstelle ungleich Null, dann wissen wir, dass sich dort ein Extrempunkt befindet.
Für die zweite Ableitung an einer potentiellen Extremstelle \(f''(x_E)\) kann folgendes rauskommen:
- \(f''(x_E)\lt 0\,\,\implies\,\,x_E\) ist ein Hochpunkt
- \(f''(x_E)\gt 0\,\,\implies\,\,x_E\) ist ein Tiefpunkt
- \(f''(x_E)= 0\,\,\implies\,\,x_E\) ist kein Extrempunkt
Hinreichende und Notwendige Bedingung für Extremstellen
1. Notwendige Bedingung:
\(f'(x_E)=0\)
\(\implies\) potentielle Extremstelle
2. Hinreichende Bedingung:
\(f'(x_E)=0\)
und
\(f''(x_E)\ne 0\)
\(\implies\) Extremstelle
Achtung !
Besitzt eine Funktion mehrere potentielle Extremstellen, so kann die Funktion auch mehrere Extremstellen besitzen. Wenn eine Funktion mehrere Hochpunkte und/oder Tiefpunkte besitzt, so unterscheidet man zwischen Globalen und Lokalen Extremstellen.
Beispiel 1 zu Extremstellen
Untersuche die Funktion
\(f(x)=x^3-6x^2+9x-2\)
auf Extremstellen.
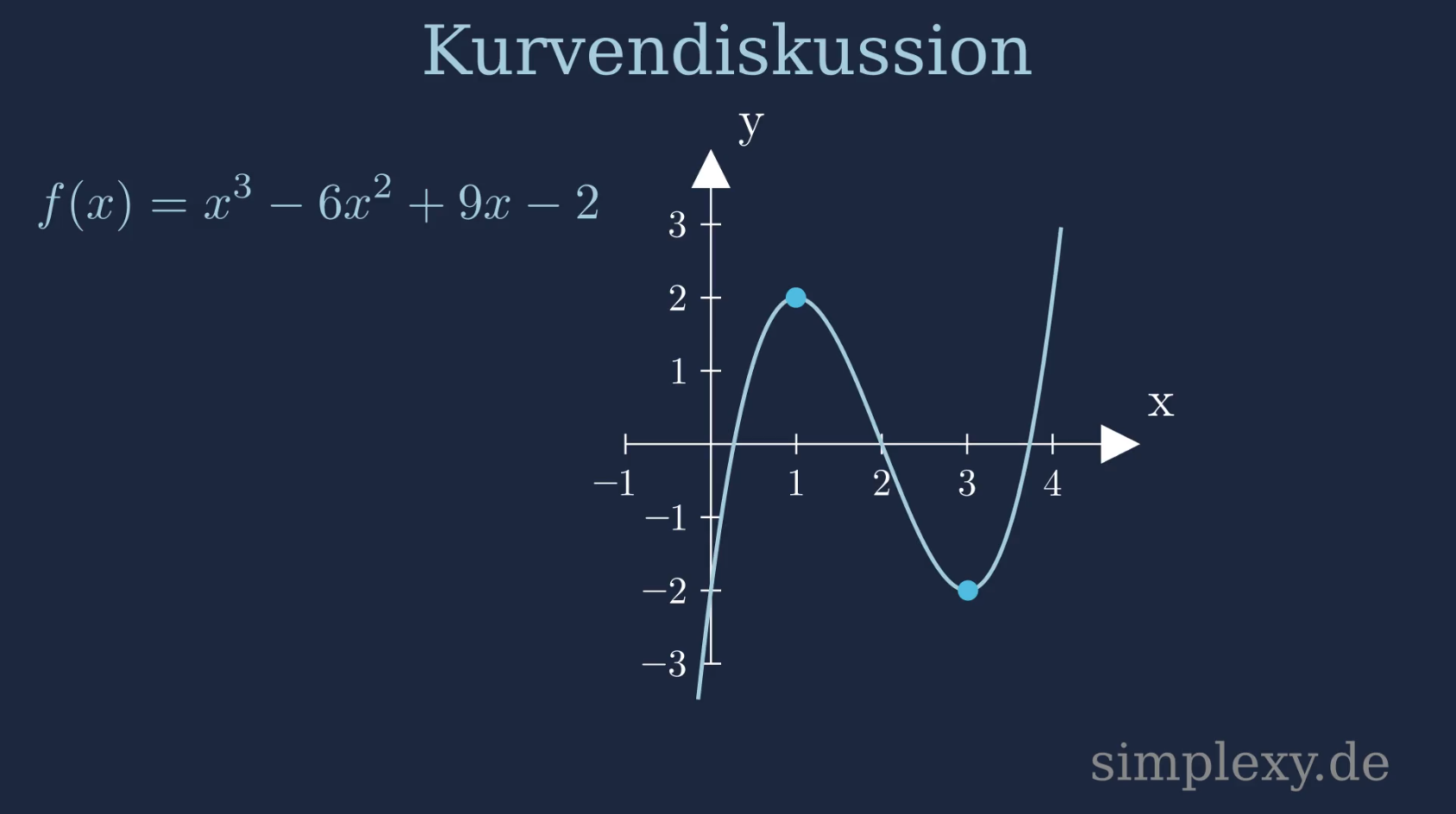
Um die Extrempunkte der Funktion zu berechnen, müssen wir zunächst die erste Ableitung der Funktion berechnen.
\(f'(x)=3x^2-12x+9\)
Nun wo wir die Ableitung der Funktion berechnet haben, können wir raus finden, an welchen Stellen die Steigung der Funktion null ist. Nur an Stellen, an denen die Funktion eine Steigung von null besitzt, kann eine Extremstelle vorhanden sein. Die Steigung der Funktion und die erste Ableitung der Funktion sind äquivalent. Um raus zu finden, wo die Funktion eine Steigung von null besitzt, können wir die Ableitung der Funktion null setzen.
\(f'(x)=3x^2-12x+9=0\)
Wir haben also nun die quadratische Gleichung
\(3x^2-12x+9=0\)
die wir mit der Mitternachtsformel oder der pq-Formel lösen können.
Mit dem Rechner von Simplexy kann diese quadratische Gleichung ebenfalls gelöst werden. Wir erhalten die Lösungen
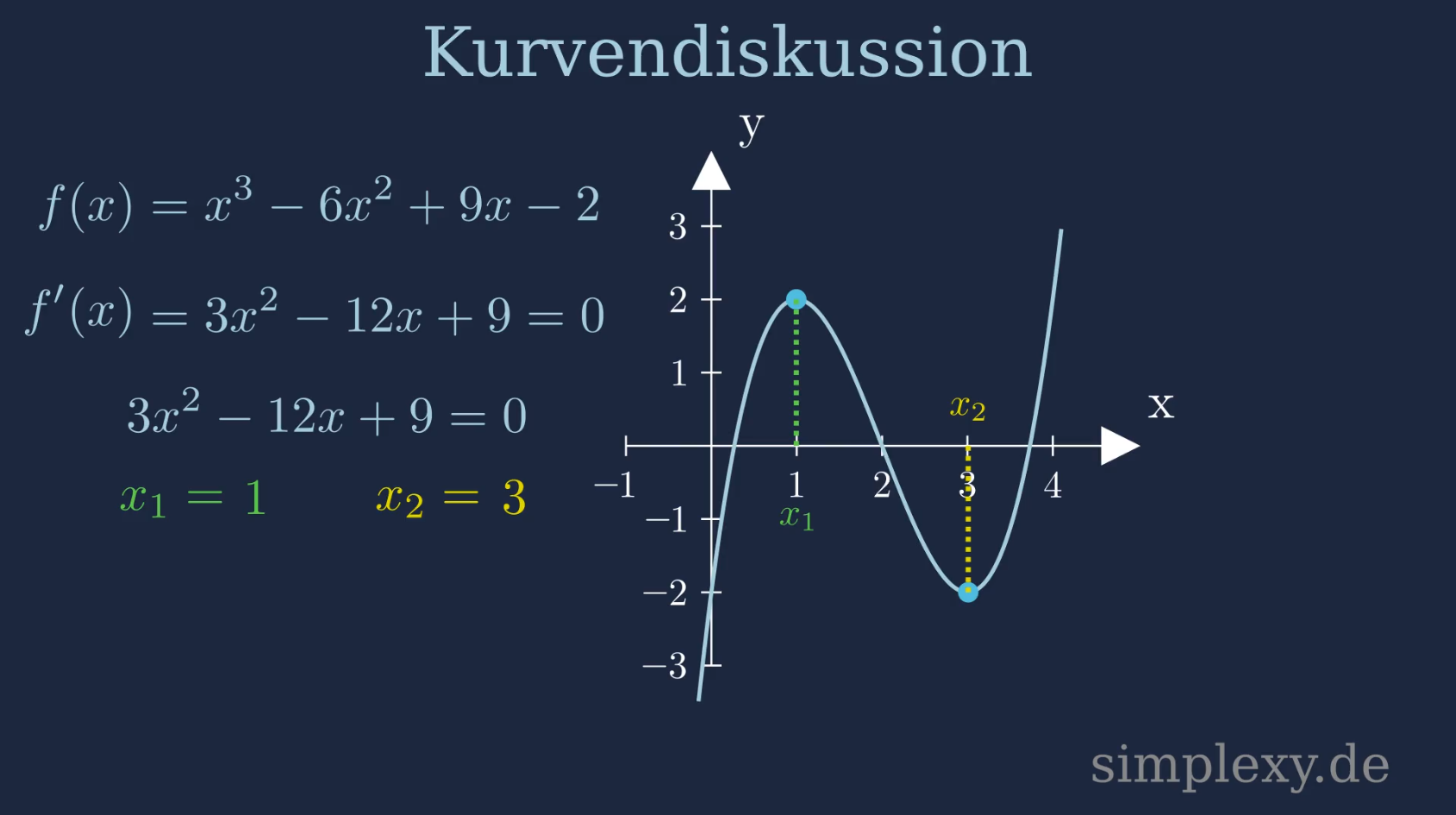
\(x_1=1\)
und
\(x_2=3\)
Damit haben wir nun zwei potentielle Extrempunkte. Um raus zu finden ob ein potentieller Extrempunkt auch wirklich ein Extrempunkt ist, muss man die hinreichende Bedingung überprüfen. Aus dem Graphen der Funktion können wir aber sehen, dass es sich hierbei wirklich um Extrempunkte handelt.
Möchte man trotzallem die hinreichende Bedingung überprüfen, so muss man die zweite Ableitung der Funktion berechnen und dort die jeweiligen x-Werte der potentiellen Extremstellen einsetzen.
\(f''(x)=6x-12\)
Nun müssen wir \(x_1\) und \(x_2\) in die zweite Ableitung einsetzen.
\(f''(x_1)=6\cdot 1-12=-6\)
Da \(f''(x_1)\neq 0\) ist, ist die Hinreichende Bedingung erfüllt. Darüber hinaus ist \(f''(x_1)\lt 0\) und damit liegt dort ein Maximum vor.
Jetzt können wir \(x_2\) in die zweite Ableitung einsetzen.
\(f''(x_2)=6\cdot 3-12=6\)
Da \(f''(x_2)\neq 0\) ist, ist die Hinreichende Bedingung erfüllt. Darüber hinaus ist \(f''(x_2)\gt 0\) und damit liegt dort ein Minimum vor.
Wir wissen also nun, dass an der Stelle \(x_1\) ein Maximum und an der Stelle \(x_2\) ein Minimum vorliegt. Wir müssen jetzt nur noch die jeweiligen \(y-\)Werte berechnen.
Dazu setzen wir \(x_1\) und \(x_2\) in unsere Ausgangsfunktion
\(f(x)=x^3-6x^2+9x-2\)
Setzen wir zunächst \(x_1\) ein:
\(\begin{aligned} y_1&=f(x_1)=1^3-6\cdot 1^2+9\cdot 1-2\\ &=2 \end{aligned}\)
jetzt setzen wir \(x_2\) ein:
\(\begin{aligned} y_2&=f(x_2)=3^3-6\cdot 3^2+9\cdot 3-2\\ &=-2 \end{aligned}\)
Die Funktion besitzt bei
\((1|2)\) ein Hochpunkt
und bei
\((3|-2)\) ein Tiefpunkt.

Wenn man den Graphen einer Funktion nicht einzeichnen kann, so muss man bei der Berechnung von Extremstellen immer die Notwendige und die hinreichende Bedingung betrachten.
Beispiel 2 zu Extrempunkten
Untersuche die Funktion
\(f(x)=\frac{1}{12}x^3+x^2\)
auf Extremstellen.
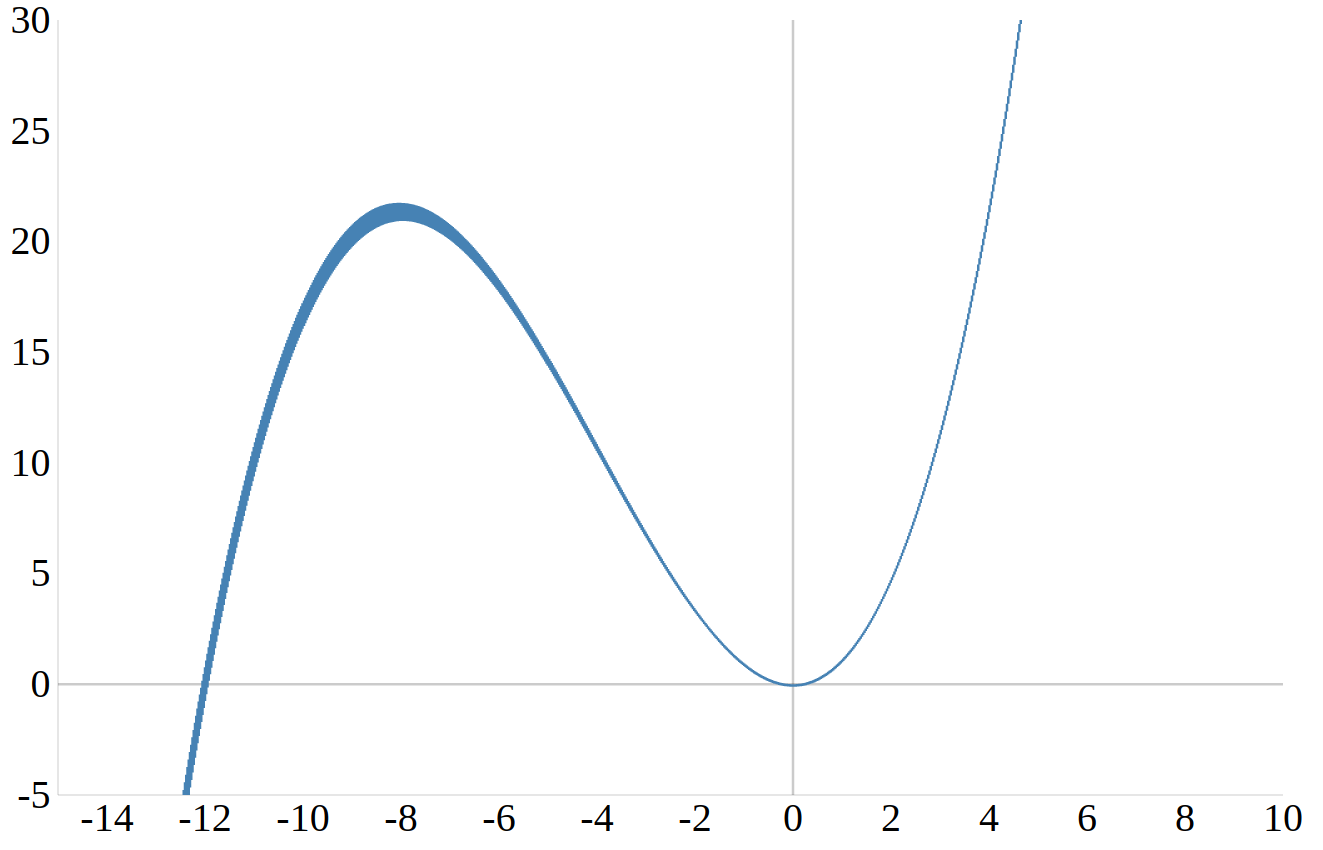
Schritt 1 - Bilde die erste Ableitung und setze sie gleich Null:
\(f'(x)=\frac{1}{4}x^2+2x=0\)
Löst man diese Gleichung mit der pq-Formel, dann erhält man als potentielle Extremwerte
\(x_1=0\) und \(x_2=-8\)
Schritt 2 - Berechne die zweite Ableitung und setze \(x_1\) und \(x_2\) ein:
\(f''(x)=\frac{1}{2}x+2\)
- \(x_1\) einsetzen:
- \(x_2\) einsetzen:
\(f''(x_1)=\frac{1}{2}\cdot 0 +2\gt 0\)
\(\implies\)
\(x_1\) ist ein Minimum
\(f''(x_2)=\frac{1}{2}\cdot (-8) +2\lt 0\)
\(\implies\)
\(x_2\) ist ein Maximum
Schritt 3 - Die Extrempunkte in die Ausgangsfunktion einsetzten:
\(y_1=f(x_1)=0\)
\(y_2=f(x_2)=\frac{64}{3}\)
Die Funktion besitzt bei
\((0|0)\) ein Minimum
und bei
\((-8|\frac{64}{3})\) ein Maximum.
Mit dem Rechner von Simplexy kannst du die Hochpunkte und Tiefpunkte einer Funktion berechnen und so dein Rechenweg überprüfen.
Arten von Extrempunkten
Wir haben nun sowohl Maxima (Hochpunkte) als auch Minima (Tiefpunkte) behandelt. Extrempunkte werden jedoch noch in global und lokal unterschieden.

Ein lokaler Extrempunkt ist nur in einer bestimmten Umgebung der "höchte" bzw. "tiefste" Punkt eines Graphen. In der oberen Abbildung ist der Graph einer Funktion abgebildet. In grün ist ein lokales Maximum eingezeichnet. Man sieht deutlich, dass dieser Punkt in einer bestimmten Umgebung der höchste Funktionswert besitzt. Es ist jedoch nicht der absolut höchste Punkt des Graphen.
Ein globaler Extrempunkt ist ein Maximum bzw. ein Minimum mit der Eigenschaft, dass es der "höchste" bzw. "tiefste" punkt des Graphen ist. Es findet sich kein weiterer Funktionswert der größer bzw. kleiner als das globalen Extremum ist. Dazu muss man das asymptotische Verhalten der Funktion betrachten. Man muss nachweisen, das für
\(x\rightarrow \infty\)
&
\(x\rightarrow -\infty\)
kein weiterer Funktionswert größer bzw. kleiner ist als die zu untersuchende Extremstelle. In der oberen Abbildung ist ein globales Minimum (Rot) dargestellt.
