Hochpunkt und Tiefpunkt Berechnen
Hochpunkt und Tiefpunkt Rechner
Der Online Rechner von Simplexy kann dir bei der Berechnung von Hochpunkten und Tiefpunkten helfen. Mit dem Rechner kannst du dir den Graphen einer Funktion zeichnen lassen, die Funktion ableiten und viel mehr.
Hochpunkt und Tiefpunkt berechnen
In dem folgenden Video findest du ein Beispiel zur Berechnung vom Hochpunkt und Tiefpunkt einer Funktion.
Um raus zu finden ob eine Funktion Hochpunkte oder Tiefpunkte besitzt, muss man die notwendige und die hinreichende Bedingung für die Existenz von Extremstellen betrachten.
1. Notwendige Bedingung:
\(f'(x_E)=0\)
\(\implies\)
potentielle Extremstelle bei \(x_E\)
Ist die erste Ableitung einer Funktion an der Stelle \(x_E\) gleich Null, dann befindet sich dort ein potentieller Hochpunkt oder Tiefpunkt. Um sicher zu gehen, dass es sich wirklich um eine Extremstelle handelt, muss man die hinreichende Bedingung betrachten.
2. Hinreichende Bedingung:
\(f'(x_E)=0\) und \(f''(x_E)\ne 0\)
\(\implies\)
Extremstelle bei \(x_E\).
Ist die erste Ableitung einer Funktion an einer potentiellen Extremstelle \(x_E\) null und die zweite Ableitung der Funktion an dieser potentiellen Extremstelle ungleich Null, dann wissen wir, dass sich dort ein Extrempunkt befindet. Damit weis man nur, das eine Extremstelle vorhanden ist, man weis nicht ob es sich um einen Hochpunkt oder einen Tiefpunkt handelt. Dazu muss man die potentiellen Extremstelle in die zweite Ableitung einsetzen.
Für die zweite Ableitung an einer potentiellen Extremstelle \(f''(x_E)\) kann folgendes rauskommen:
- \(f''(x_E)\lt 0\,\,\implies\,\,x_E\) ist ein Hochpunkt
- \(f''(x_E)\gt 0\,\,\implies\,\,x_E\) ist ein Tiefpunkt
- \(f''(x_E)= 0\,\,\implies\,\,x_E\) ist kein Extrempunkt
Hinreichende und Notwendige Bedingung für Hochpunkt oder Tiefpunkt
1. Notwendige Bedingung:
\(f'(x_E)=0\)
\(\implies\) potentielle Extremstelle
2. Hinreichende Bedingung:
\(f'(x_E)=0\)
und
\(f''(x_E)\ne 0\)
\(\implies\) Hochpunkt oder Tiefpunkt
Ein Hochpunkt liegt vor wenn:
\(f''(x_E)\lt 0\)
Ein Tiefpunkt liegt vor wenn:
\(f''(x_E)\gt 0\)
Beispiel zu Hochpunkt und Tiefpunkt Berechnung
Berechne die Koordinaten vom Hochpunkt und vom Tiefpunkt für die Funktion
\(f(x)=x^3-6x^2+9x-2\)
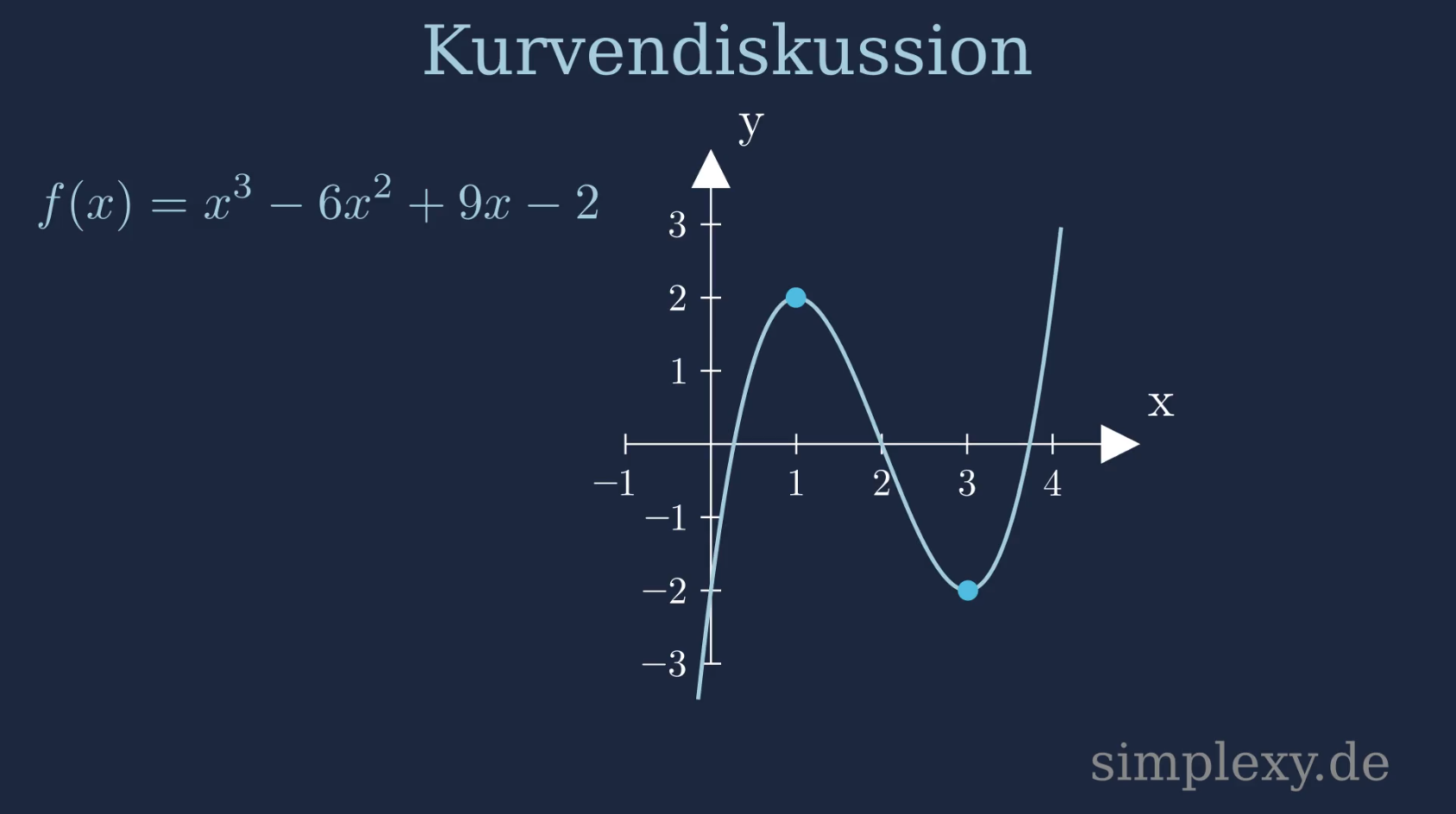
Um den Hochpunkt und Tiefpunkt der Funktion zu berechnen, müssen wir die erste Ableitung der Funktion berechnen.
\(f'(x)=3x^2-12x+9\)
Die Hochpunkte und Tiefpunkte einer Funktion liegen dort, wo die Steigung der Funktion null ist. Wir können also nun die erste Ableitung der Funktion null setzen:
\(f'(x)=3x^2-12x+9=0\)
Damit erhalten wir eine quadratische Gleichung
\(3x^2-12x+9=0\)
Mittels pq-Formel oder Mitternachtsformel können wir diese Gleichung lösen.
Eine quadratische Gleichung kann bis zu zwei Lösungen besitzen. Das wird hier der Fall sein, denn unsere Funktion hat einen Hochpunkt und einen Tiefpunkt.
\(x_1=1\)
und
\(x_2=3\)
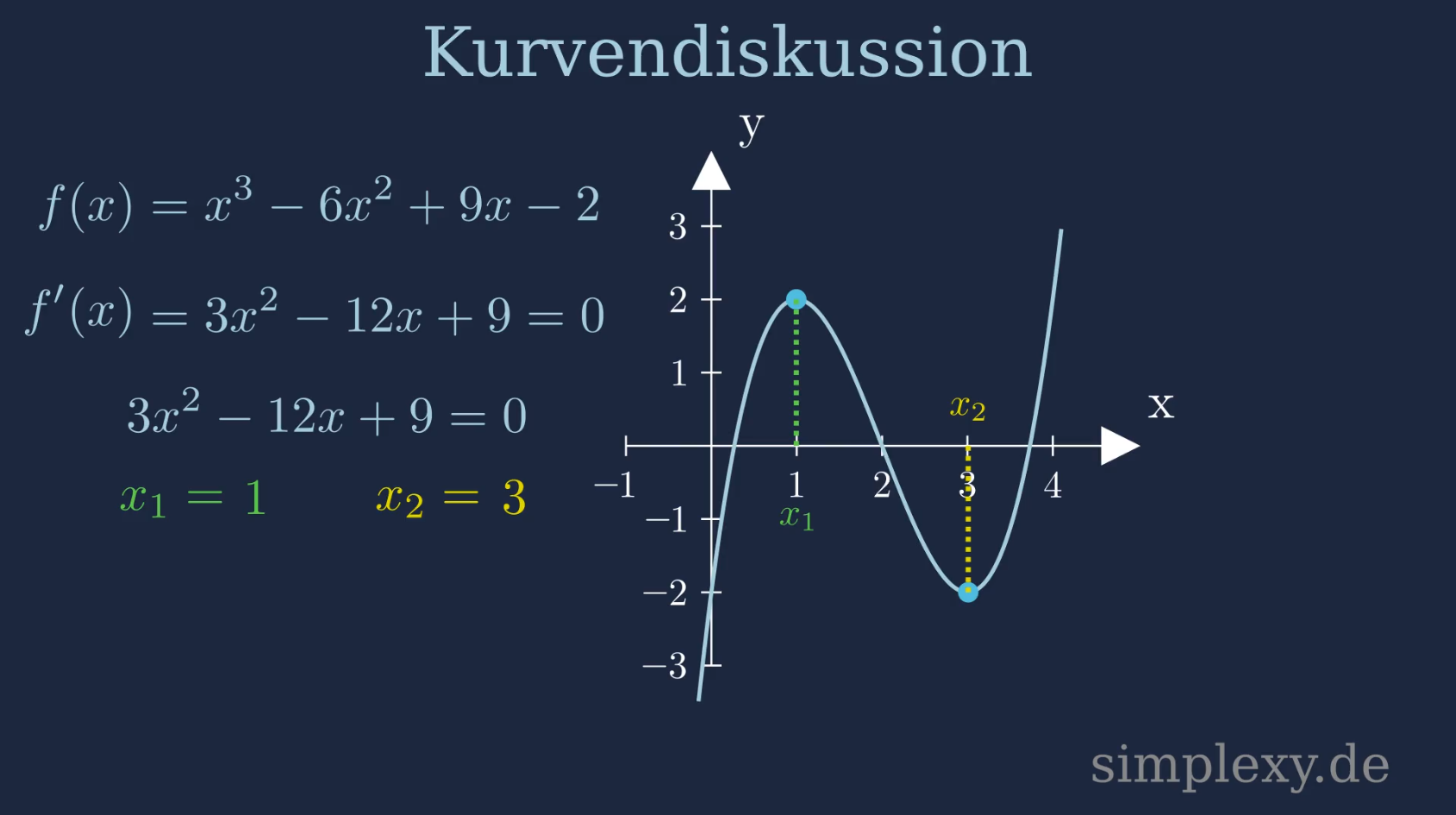
Wir sehen an dem Grapen der Funktion, das an der Stelle \(x_1=1\) ein Hochpunkt liegt und an der Stelle \(x_2=3\) ein Tiefpunkt. Normalerweise muss man bei der Berechnung von Hoch- und Tiefpunkten die notwendige und hinreichende Bedingung untersuchen. Wir haben bis jetzt nur gezeigt, das die Notwendige Bedingung erfüllt ist. Im Graphen sehen wir aber eindeutig wo der Hochpunkt und wo der Tiefpunkt liegt. Hier muss man die hinreichende Bedingung nicht zwangsläufig durchführen.
Trotzallem ist es ratsam die hinreichende Bedingung zu überprüfen, dazu brauchen wir die zweite Ableitung der Funktion:
\(f''(x)=6x-12\)
Nun werden wir \(x_1\) und \(x_2\) in die zweite Ableitung einsetzen.
\(f''(x_1)=6\cdot 1-12=-6\)
Da \(f''(x_1)\lt 0\) ist, liegt hier ein Hochpunkt vor.
Jetzt können wir \(x_2\) in die zweite Ableitung einsetzen.
\(f''(x_2)=6\cdot 3-12=6\)
Da \(f''(x_2)\gt 0\) ist, liegt hier ein Tiefpunkt vor.
Zum Schluss müssen wir die \(y\)-Werte vom Hochpunkt und vom Tiefpunkt berechnen.
Dazu setzen wir \(x_1\) und \(x_2\) in unsere Funktion
\(f(x)=x^3-6x^2+9x-2\)
Setzen wir zunächst \(x_1\) ein:
\(\begin{aligned} y_1&=f(x_1)=1^3-6\cdot 1^2+9\cdot 1-2\\ &=2 \end{aligned}\)
jetzt setzen wir \(x_2\) ein:
\(\begin{aligned} y_2&=f(x_2)=3^3-6\cdot 3^2+9\cdot 3-2\\ &=-2 \end{aligned}\)
Die Funktion besitzt bei
\((1|2)\) ein Hochpunkt
und bei
\((3|-2)\) ein Tiefpunkt.

Es ist ratsam die hinreichende Bedingung zu überprüfen, auch wenn man den Graphen der Funktion gezeichnet hat und die Hochpunkte bzw. Tiefpunkte sehen kann.
Lokale und Globale Extrempunkte
Bis jetzt haben wir zwei Arten von Extrempunkten kennen gelernt. Zum einen gibt es Hochpunkte und zum anderen Tiefpunkte. Diese zwei werden jedoch nochmals in globale und lokale Extrema unterschieden.

Ein lokaler Hochpunkt bzw. Tiefpunkt ist ein Punkt auf einer Funktion, in dessen Umgebung kein weiterer Punkt "höher" bzw. "tiefer" liegt. Wichtig ist hier, dass diese Bedingung lediglich in einer bestimmten Umgebung erfüllt ist. In dem oberen Bild ist ein lokaler Hochpunkt (Grün) eingezeichnet. In der Umgebung um den Hochpunkt findet sich kein weiterer Punkt der höher liegt. Man sieht aber leicht, das dieser lokale Hochpunkt nicht der "höchste Punkt" der Funktion ist. Daher ist es nur ein lokaler Hochpunkt. Das gleiche gilt entsprechend für einen lokalen Tiefpunkt.
Ein globaler Hochpunkt bzw. Tiefpunkt ist ein Extrempunkt der gleichzeitig der "höchste" bzw. "tiefste" Punkt der Funktion ist. Im oberen Graphen ist ein globaler Tiefpunkt (Rot) gezeigt. Es findet sich kein weiterer Punkt mit einem kleineren Funktionswert.
Ein globaler Extrempunkt ist auch immer ein lokaler Extrempunkt. Das gilt anderes herum jedoch nicht. Ein lokaler Extrempunkt ist nicht immer auch ein globaler Extrempunkt.
Um sicher zu gehen, das ein Hochpunkt oder Tiefpunkt wirklich global ist, muss man das asymptotische Verhalten der Funktion untersuchen. Es muss sichergestellt werden, das für
\(x\rightarrow \infty\)
&
\(x\rightarrow -\infty\)
kein Funktionswert "größer" bzw. "kleiner" ist.
