Binomische Formeln
Binomische Formeln Rechner
Mit dem Online Rechner von Simplexy kannst du viele Matheaufgaben berechnen und dabei den Rechenweg erhalten. Mit dem Rechner kannst du auch ganz bequem eine Binomische Formel berechnen.
Binomische Formeln erklärt
Insgesamt gibt es drei binomische Formeln. Sie bilden ein wichtiges Hilfsmittel um Terme, Gleichungen und Funktionen zu vereinfachen. Die binomischen Formeln werden zum Ausklammern und zum Faktorisieren angewandt.
Wie lautet die binomische Formel?
Die drei binomischen Formeln
1. Binomische Formel:
2. Binomische Formel:
3. Binomische Formel:
\((a+b)^2=a^2+2ab+b^2\)
\((a-b)^2=a^2-2ab+b^2\)
\((a+b)(a-b)=a^2-b^2\)
Erste binomische Formel
\((a+b)^2=a^2+2ab+b^2\)
Herleitung der 1. Binomischen Formel
\(\begin{aligned} (a+b)^2&=(a+b)\cdot (a+b)\\ &=a\cdot(a+b)+b\cdot (a+b)\\ &=a\cdot a+a\cdot b+b\cdot a+b\cdot b\\ &=a^2+a\cdot b+b\cdot a+b^2\\ &=a^2+2\cdot a\cdot b+b^2\\ \end{aligned}\)
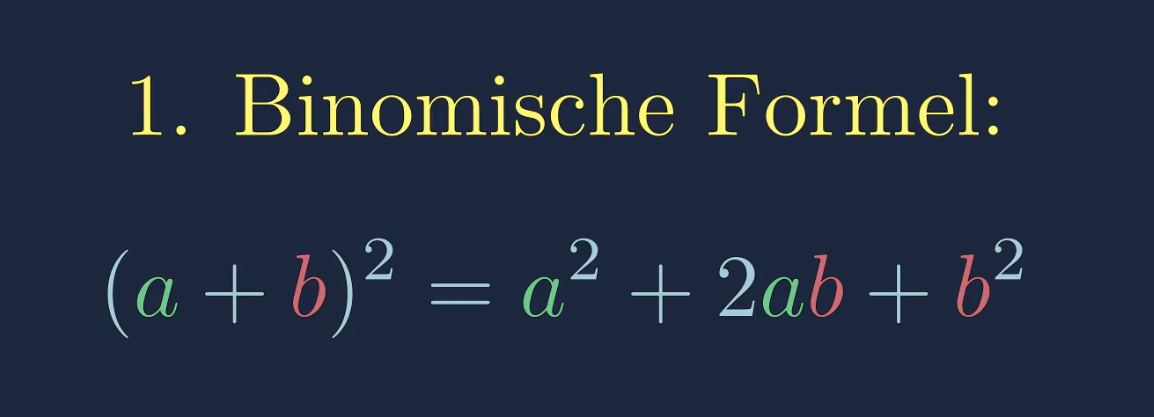
Wer sich mit der Klammerrechnung bereits auskennt, der wird feststellen, dass es sich bei der Herleitung der 1. binomischen Formel im Grunde um das Ausklammern des linken Ausdrucks handelt.
\((\textcolor{blue}{a}+\textcolor{red}{b})\cdot (\textcolor{green}{a}+\textcolor{grey}{b})=\textcolor{blue}{a}\cdot \textcolor{green}{a}+\textcolor{blue}{a} \cdot \textcolor{grey}{b}+\textcolor{red}{b}\cdot \textcolor{green}{a}+\textcolor{red}{b}\cdot \textcolor{grey}{b}\)
Erste binomische Formel Beispiele
1. Beispiel:
\((2+1)^2=2^2+2\cdot 2\cdot 1+1^2=9\)
Im oberen Beispiel haben wir die 1. binomische Formel verwendet um das Ergebnis zu berechnen. Man hätte aber ebenso gut wie folgt rechnen können:
\((2+1)^2=3^2=9\)
Sind in den Klammern nur Zahlen vorhanden, so ist es sicherlich einfacher auf die binomische Formel zu verzichten. Im Allgemeinen werden in den Klammern jedoch Variablen (Buchstaben) stehen.
2. Beispiel:
\(\begin{aligned} (2x+4)^2&=(2x)^2+2\cdot 2x\cdot 4+4^2\\ &=4x^2+16x+16 \end{aligned}\)
Um Beispiel 2 zu lösen, verwendet man die 1. Binomische Formel
\((a+b)^2=a^2+2ab+b^2\)
Dabei ist \(a=2x\) und \(b=4\). Um auf die Lösung zu kommen, muss man diese Werte lediglich in die binomische Formel einsetzen. Solche Terme kann man ganz bequem auch mit dem Online Rechner von Simplexy vereinfachen. Im Rechner kann man den Ausdruck für die binomischen Formel eingeben und erhält das Ergebnis und den Lösungsweg.
3. Beispiel:
\(\begin{aligned} (2+x)^2&=2^2+2\cdot 2\cdot x+x^2\\ &=4+4x+x^2 \end{aligned}\)
In den Beispielen haben wir stets die Rechenschritte explizit aufgeschrieben. Der mittlere Schritt muss nicht unbedingt immer aufgeschrieben werden. Wer schnell im Kopfrechnen ist, kann den mittleren Rechenschritt auch getrost weglassen und direkt das Ergebnis hinschreiben.
Zweite binomische Formel
\((a-b)^2=a^2-2ab+b^2\)
Bei der zweiten binomischen Formel hat man zwischen den Einträgen \(a\) und \(b\) ein Minus zu stehen. Wegen dem Minus wird die zweite binomische Formel auch Minus-Formel genannt.
Herleitung der 2. Binomischen Formel
\(\begin{aligned} (a-b)^2&=(a-b)\cdot (a-b)\\ &=a\cdot(a-b)-b\cdot (a-b)\\ &=a\cdot a-a\cdot b-b\cdot a+(-b)\cdot (-b)\\ &=a^2-a\cdot b-b\cdot a+b^2\\ &=a^2-2\cdot a\cdot b+b^2\\ \end{aligned}\)

Wie man sieht liegt der einzige unterschied zwischen der 1. und der 2. Binomischen Formel am Vorzeichen in der Klammer.
Zweite binomische Formel Beispiele
1. Beispiel:
\(\begin{aligned} (2x-4)^2&=(2x)^2-2\cdot 2x\cdot 4+4^2\\ &=4x^2-16x+16 \end{aligned}\)
Um Beispiel 1 zu lösen, verwendet man die 2. Binomische Formel
\((a-b)^2=a^2-2ab+b^2\)
Dabei ist \(a=2x\) und \(b=4\), man muss diese Werte lediglich in die binomische Formel einsetzen um auf die Lösung zu kommen.
2. Beispiel:
\(\begin{aligned} (2-x)^2&=2^2-2\cdot 2\cdot x+x^2\\ &=4-4x+x^2 \end{aligned}\)
3. Beispiel:
\(\begin{aligned} (3-2x)^2&=3^2-2\cdot 3\cdot 2x+(2x)^2\\ &=9-12x+4x^2 \end{aligned}\)
Dritte binomische Formel
\((a+b)(a-b)=a^2-b^2\)
Die letzte binomische Formel wird verwendet um Klammern mit einander zu multiplizieren. Die dritte binomische Formel ist im Grunde einfache Klammerrechnung. Bei der 3. binomischen Formel steht einmal ein Pluszeichen und einmal ein Minuszeichen zwischen \(a\) und \(b\). Daher wird die dritte Binomische Formel oft Plus-Minus-Formel genannt.
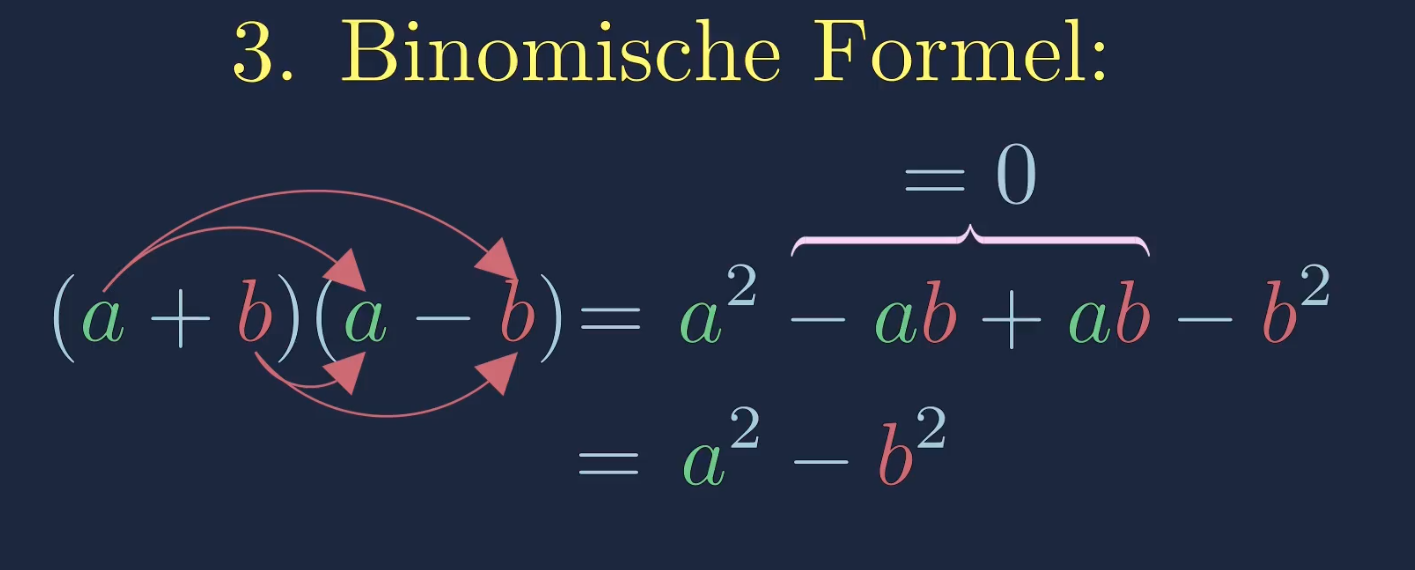
Herleitung der 3. Binomischen Formel
\(\begin{aligned} (a+b)(a-b)&=a\cdot (a-b)+b\cdot (a-b)\\ &=a\cdot a-a\cdot b+b\cdot a+b\cdot (-b)\\ &=a^2-a\cdot b+b\cdot a-b^2\\ &=a^2-b^2\\ \end{aligned}\)
Im letzten Schritt der Herleitung kürzen sich die Terme weg.
\(-a\cdot b+b\cdot a=0\)
Die zwei Terme ergeben zusammen Null, und fallen damit weg. Wir gucken und jetzt einpaar Beispiele zur 3. Binomischen Formel an.
Dritte binomische Formel Beispiele
1. Beispiel:
\(\begin{aligned} (x+2)(x-2)&=x^2-2^2=x^2-4 \end{aligned}\)
2. Beispiel:
\(\begin{aligned} (3+2x)(3-2x)&=3^2-(2x)^2=9-4x^2 \end{aligned}\)
3. Beispiel:
\(\begin{aligned} (1-3x)(1+3x)&=1^2-(3x)^2=1-9x^2 \end{aligned}\)
Die drei binomischen Formeln sind sehr hilfreiche Formeln. Sie ersparen sehr viel Zeit beim Ausklammern und beim Klammer ausmultiplizieren. Die binomischen Formeln sind vorallem dann praktisch, wenn man mit Buchstaben rechnen muss.
