Quadratische Funktionen Nullstelle berechnen
Nullstellen Rechner
Mit dem Nullstellenrechner von Simplexy kannst du ganz einfach die Nullstelle einer quadratischen Funktion berechnen, eine Parabel zeichnen lassen, die Mitternachtsformel und die pq-Formel online berechnen uvm.
Nullstelle quadratische Funktion
Parabeln kann man in vier Formen unterteilen
\(f(x)=ax^2\)
\(f(x)=ax^2+c\)
\(f(x)=ax^2+bx\)
\(f(x)=ax^2+bc+c\)
Je nach Form ergeben sich vier Fälle die man beachten muss. Um die Nullstelle einer Parabel berechnen zu können, muss man die Funktionsgleichung Null setzen. Denn die Nullstelle einer quadratischen Funktion ist stets beim y-Wert \(y=0\). In einigen Fällen benutzt man statt \(y\) auch die Schreibweise \(f(x)\), die zwei Schreibweisen bedeuten das gleiche.
\(y=f(x)\)
Die vier Formen von quadratischen Funktionen führen dazu das eine Parabel entweder keine, eine oder zwei Nullstellen besitzen kann.
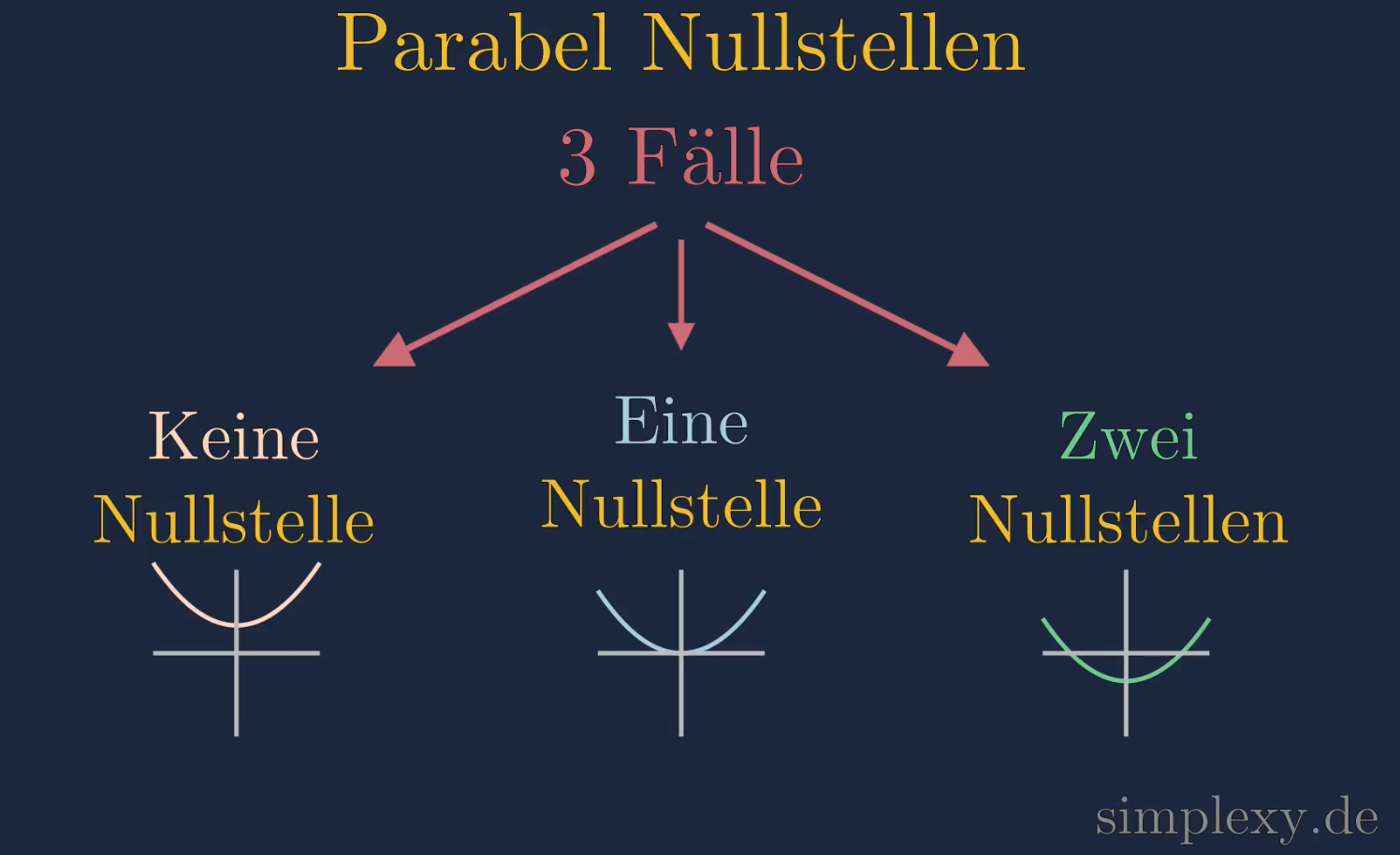
1. Fall Parabel Nullstelle
Die einfachste Form einer quadratischen Funktion lautet:
\(f(x)=ax^2\)
In diesem Fall besitzt die Parabel eine einzige Nullstelle.
Beispiele
\(f(x)=x^2\)
\(f(x)=2x^2\)
\(f(x)=-3x^2\)
\(f(x)=\frac{1}{2}x^2\)
\(f(x)=-\frac{3}{4}x^2\)
Die Nullstelle einer Parabel in dieser Form ist stets bei \(x_0=0\). Der \(y-\)Wert ist selbstverständlich ebenfalls bei \(y=0\). Möchte man die Koordninaten der Nullstelle angeben, so schreibt man:
\(x_0=(0|0)\)
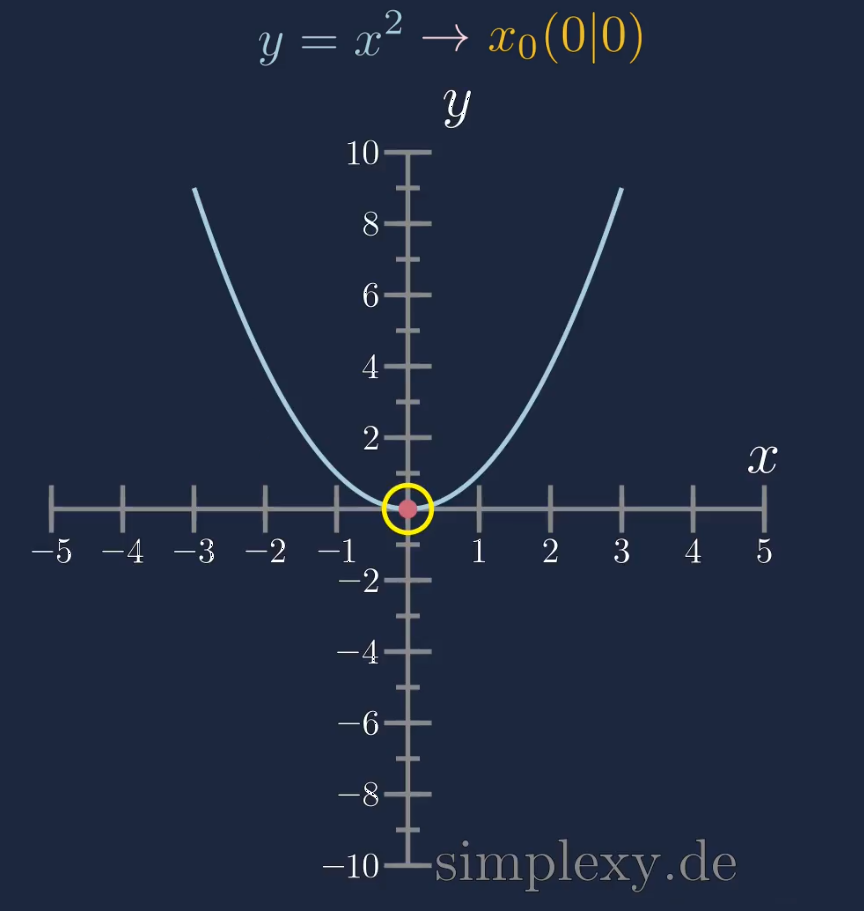
2. Fall quadratische Funktion Nullstelle
Eine quadratische Funktion der Form
\(f(x)=ax^2+c\)
Kann eine oder zwei Nullstellen besitzen.
Um die Parabel Nullstelle berechnen zu können, muss man die Funktionsgleichung Nullsetzen und zunächst nach \(x^2\) auflösen. Anschließend muss man die Wurzel ziehen.
1. Beispiel Nullstelle berechnen
Gegeben ist die quadratische Funktions
\(f(x)=x^2-4\)
Kannst du die Nullstellen berechnen?
Lösung
Zunächst müssen wir die Funktionsgleichung der Parabel Nullsetzen:
\(0=x^2-4\)
Anschließend müssen wir die Gleichung nach \(x^2\) umstellen und die Wurzel ziehen:
\(\begin{aligned} 0&=x^2-4\,\,\,\,|+4\\ 4&=x^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\sqrt{\hspace{1em}}\\ \sqrt{4}&=\sqrt{x^2}\\ \sqrt{4}&=x\\ \end{aligned}\)
Nun muss man wissen das Wurzel von Vier zwei lösungen besitzt. Es gilt:
\(\sqrt{4}=2\) und \(\sqrt{4}=-2\)
Damit hat man also
\(2=x\)
und
\(-2=x\)
Es existieren also zwei Nullstellen, die eine liegt bei \(x_1=2\) und die andere bei \(x_2=-2\).
2. Beispiel Nullstelle berechnen
Berechne die Nullstellen der quadratischen Funktion
\(f(x)=x^2+8\)
Lösung
Zunächst müssen wir die Funktionsgleichung Null setzen:
\(0=x^2+8\)
Anschließend müssen wir die Gleichung nach \(x^2\) umstellen und die Wurzel ziehen:
\(\begin{aligned} 0&=x^2+8\,\,\,\,|-8\\ -8&=x^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,|\sqrt{\hspace{1em}}\\ \sqrt{-8}&=\sqrt{x^2}\\ \sqrt{-8}&=x\\ \end{aligned}\)
Nun muss man die Wurzel von \(-8\) berechnen. Die Wurzel einer negativen Zahl ist (in den Reellen Zahlen \(\mathbb{R}\)) nicht definiert!
Wir müssen also hier die Rechnung abbrechen und sagen, die Funktion besitzt keine Nullstellen. Die Parabel befindet sich vollständig oberhalb der x-Achse.
3. Fall
\(f(x)=ax^2+bx\)
In solch einem Fall beginnt man damit das \(x\) auszuklammern und anschließend nutzt man den Satz vom Nullprodukt um die Parabel Nullstellen berechnen zu können.
Beispiel 1
Berechne die Nullpunkte bzw. Nullstellen der quadratischen Funktion
\(f(x)=x^2+8x\)
Lösung
Als erstes muss man ein x ausklammern
\(f(x)=x^2+8x=x\cdot(x+8)\)
Nun muss man die Funktion Null setzen:
\(0=x\cdot(x+8)\)
An der Stelle können wir den Satz vom Nullprodukt anwenden um die Nullstellen der Parabel zu ermitteln. Dazu teilen wir die Gleichung in zwei Faktoren:
\(0=\underbrace{x}_{1. Faktor}\cdot(\underbrace{x+8}_{2. Faktor})\)
Der Satz vom Nullprodukt sagt: "Ein Produkt ist genau dann Null, wenn einer der Faktoren gleich Null ist".
Wir Können also beide Faktorn getrennt gleich Null setzen.
1 Faktor:
\(x=0\)
\(\implies x_1=0\)
Die erste Nullstelle befindet sich somit beim \(x-\)Wert \(x_1=0\).
2 Faktor:
\(\begin{aligned} x+8&=0\\ x+8&=0\,\,\,\,\,\,\,\,\,\,|-8\\ x&=-8\\ \\ \\ \implies x_2&=-8 \end{aligned}\)
Die zweite Nullstelle befindet sich somit beim \(x-\)Wert \(x_2=-8\).
Beispiel 2
Gegeben ist die quadratische Funktion
\(f(x)=2x^2-4x\)
Wo liegen die Nullstellen der Parabel?
Lösung
Zunächst muss man das x ausklammern
\(f(x)=2x^2-4x=x\cdot(2x-4)\)
Nun kann man die Funktion Null setzen:
\(x\cdot(2x-4)=0\)
Nun teilen wir die Gleichung wieder in zwei Faktoren:
\(\underbrace{x}_{1. Faktor}\cdot(\underbrace{2x-4}_{2. Faktor})=0\)
Wir können jetzt wieder den Satz vom Nullprodukt anwenden. Wir setzen also beide Faktorn erneut gleich Null.
1 Faktor:
\(x=0\)
\(\implies x_1=0\)
Die erste Nullstelle befindet sich somit beim \(x-\)Wert \(x_1=0\).
2 Faktor:
\(\begin{aligned} 2x-4&=0\\ 2x-4&=0\,\,\,\,\,\,\,\,\,\,|+4\\ 2x&=4\,\,\,\,\,\,\,\,\,\,|\div 2\\ x&=2\\ \\ \implies x_2&=2 \end{aligned}\)
Die zweite Nullstelle befindet sich somit beim \(x-\)Wert \(x_2=2\).
4. Fall
\(f(x)=ax^2+bx+c\)
Der vierte Fall ist der schwierigste Fall. Um hier die Nullstellen einer quadratischen Funktion berechnen zu können benötigt man die Mitternachtsformel bzw. die pq-Formel. Manchmal wird die Mitternachtsformel auch abc-Formel genannt.
Man erhält die Nullstellen einer Parabel indem man die Funktionsgleichung gleich null setzt.
\(ax^2+bx+c=0\)
Die Parabel Nullstellen kann man anschließend über die Mitternachtsformel berechnen.
Mitternachtsformel
Um die Parabel Nullstellen berechnen zu können, muss man die Mitternachtsformel anwenden. Die Mitternachtsformel gibt die Nullstellen \(x_1\) und \(x_2\) an. Die Mitternachtsformel lautet:
\(\begin{aligned} x_{1/2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Da eine Parabel bis zu zwei Nullstellen besitzen kann (\(x_1\) und \(x_2\)) gibt es eine Fallunterscheidung
Fallunterscheidung
\(\begin{aligned} x_{1}=\frac{-b\textcolor{red}{-}\sqrt{b^2-4ac}}{2a} \end{aligned}\)
\(\begin{aligned} x_{2}=\frac{-b\textcolor{blue}{+}\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Wie du siehst besitzt die Mitternachtsformel zwei Lösungen \(x_{1/2}\), denn eine quadratische Funktion kann bis zu zwei Nullstellen bestizen. Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen. Um die Anzahl an Nullstellen zu bekommen musst du die Diskriminante
\(D=b^2-4ac\)
berechnen, dass ist der Term unter der Wurzel in der Mitternachts-Formel. Es gilt:
Mitternachtsformel Diskriminante
Die Anzahl an Nullstellen einer Parabel erhältst du über die Diskriminante. Es gilt:
- Wenn \(D\) kleiner als null ist, dann besitzt die Parabel keine Nullstellen.
- Wenn \(D=0\) ist, dann besitzt die Parabel genau eine Nullstelle.
- Wenn \(D\) größer als null ist, dann besitzt die Parabel zwei Nullstellen.
Im unteren Bild sind die Graphen zweier Parabeln abgebildet, die blaue Parabel besitzt keine Nullstellen während die rote Parabel zwei Nullstellen besitzt.
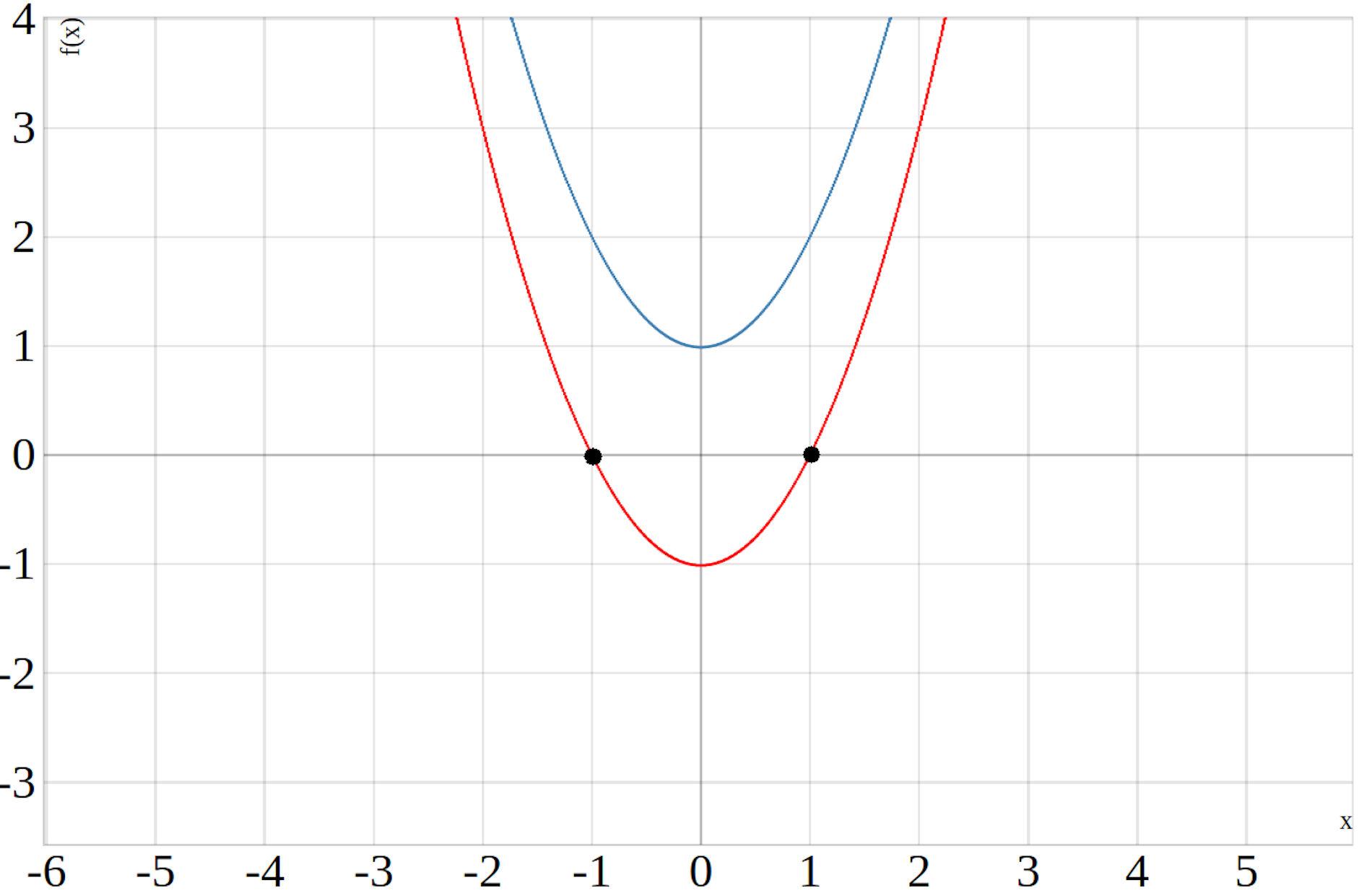
Parabel Normalform Nullstellen
Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen.
Die Nullstellen einer Parabel in der Normalform
\(f(x)=ax^2+bx+c\)
berechnen sich mit Hilfe der Mitternachtsformel:
\(\begin{aligned} x_{1/2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{aligned}\)
Vorgehen um Nullstellen einer Parabel berechnen zu können
Quadratische Funktion in die Normalform bringen.
\(a,b\) und \(c\) aus der Normalform ablesen.
\(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
Mitternachtsformel ausrechnen.
Beispiel 1:
\(f(x)=2x^2-12x-14\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=2,\) \(b=-12\) und \(c=-14\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-12)\pm\sqrt{(-12)^2-4\cdot 2\cdot (-14)}}{2\cdot 2}\\ \\ &=\frac{12\pm\sqrt{144+112}}{4}\\ \\ &=\frac{12\pm\sqrt{256}}{4}\\ \\ &=\frac{12\pm 16}{4}\\ \end{aligned}\)
Fallunterscheidung:
\(x_{1}=\)\(\frac{12-16}{4}\)\(=-1\)
\(x_{2}=\)\(\frac{12+16}{4}\)\(=7\)
Die Nullstellen der Parabel befinden sich somit bei
\(x_1=-1\) und \(x_2=7\).
Beispiel 2:
\(f(x)=4x^2-16x+16\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=4,\) \(b=-16\) und \(c=16\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ \\ &=\frac{-(-16)\pm\sqrt{(-16)^2-4\cdot 4\cdot 16}}{2\cdot 4}\\ \\ &=\frac{16\pm\sqrt{256-256}}{8}\\ \\ &=\frac{16\pm\textcolor{blue}{\sqrt{0}}}{8}\\ \\ &=\frac{16\pm 0}{8}\\ \\ &=\frac{16}{8}\\ \\ &=2\\ \end{aligned}\)
In diesem Beispiel hat die Parabel nur eine Nullstelle, da
die Diskriminante \(D\) gleich Null ist.
\(D=b^2-4ac=0\)
Die einzige Nullstelle befindet sich bei \(x_0=2\).
Beispiel 3:
\(f(x)=2x^2-8x+11\)
Die Funktion befindet sich bereits in der Normalform. Wir können also direkt zum zweiten Schritt übergehen und \(a,b\) und \(c\) ablesen.
\(a=2,\) \(b=-8\) und \(c=11\)
Nun müssen wir \(a,b\) und \(c\) in die Mitternachtsformel einsetzen.
\(\begin{aligned} x_{1/2}&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ &=\frac{-(-8)\pm\sqrt{(-8)^2-4\cdot 2\cdot 11}}{2\cdot 2}\\ &=\frac{8\pm\sqrt{64-88}}{4}\\ &=\frac{16\pm\textcolor{red}{\sqrt{-24}}}{4}\\ \end{aligned}\)
In diesem Beispiel hat die Parabel keine Nullstelle. Die Wurzel einer negativen Zahl ist in den reellen Zahlen nicht definiert. Aus diesem Grund hat die quadratische Funktionen keine Nullstellen. Sie befindet sich oberhalb der \(x-\)Achse.
Nutze den Rechner von Simplexy um die Nullstellen einer quadratischer Funktionen zu ermitteln. Gib dazu am besten zur Probe mal \(x^2+2x-5=0\) ein, du erhältst die Nullstellen und den Rechenweg.
Hier kommst du zum Rechner.
