Fadenpendel Geschwindigkeit
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Fadenpendel Zusammenfassung
Die Schwingungsgleichung vom Fadenpendel kann über die Betrachtung der Rückstellkraft ermittelt werden. Dabei ist die Rückstellkraft gerade die Tangentialkomponente der Gewichtskraft.
Die Schwingungsgleichung vom Fadenpendel lautet:
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}\cdot x(t)=0 \end{aligned}\)
Dabei ist:
\(x(t)\) die Auslenkung.
\(l\) die Länge des Fadens.
\(g\) die Fallbeschleunigung.
Das Fadenpendel schwingt harmonisch mit der Ort-Zeit-Funktion
\(x(t)=x_0\cdot cos(\omega\cdot t)\)
Dabei ist \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(x_0\) ist die Startauslenkung des Pendels.
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
Die Schwingungsdauer bzw. die Periodendauer berechnet sich über
Die Frequenz berechnet sich über
\(\begin{aligned} T=\frac{2\pi}{\omega} \end{aligned}\)
\(\begin{aligned} T=2\pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
\(\begin{aligned} f=\frac{1}{T} \end{aligned}\)
Fadenpendel Geschwindigkeit
In dem unteren Video ist die Geschwindigkeit vom Fadenpendel leicht erklärt.
In dem Beitrag über die Schwingungsgleichung des Fadenpendels haben wir die Ort-Zeit-Funktion des Pendels berechnet. Dort haben wir rausgefunden, dass sich das Pendel harmonisch mit der Ort-Zeit-Funktion
\(x(t)=x_0\cdot cos(\omega\cdot t)\)
bewegt. Dabei ist \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
\(x_0\) ist die Startauslenkung (Amplitude) der Schwingung.
Sobald das Fadenpendel losgelassen wird, beschleunigt es sich in Richtung der Ruhelage. Aufgrund der Trägheit fliegt der Pendelkörper durch die Ruhelage hindurch und gelangt zum anderen Umkehrpunkt. Dort kommt das Pendel für einen kurzen Moment zum Stillstand, und wird anschließend wieder in Richtung der Ruhelage beschleunigt.
Beim Durchgang durch die Ruhelage ist die Geschwindigkeit des Pendels maximal und an den Umkehrpunkten ist die Geschwindigkeit Null \((v=0)\).
Um den zeitlichen Verlauf der Geschwindigkeit zu erhalten können wir die Ort-Zeit-Funktion \(x(t)\) nach der Zeit ableiten, denn Allgemein lässt sich die Geschwindigkeit eines Körpers immer ausrechnen über:
Geschwindigkeit
\(v=\)\(\frac{\Delta x}{\Delta t}\)
bzw.
\(v=\dot{x}=\)\(\frac{dx}{dt}\)
Um den zeitlichen Verlauf der Geschwindigkeit zu ermitteln müssen wir also die Ort-Zeit-Funktion des Pendels einmal nach der Zeit ableiten.
\(\dot{x}(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Geschwindigkeit vom Fadenpendel
\(v(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Hinweis:
Für die Ableitung muss man die Kettenregel anwenden.
Dafür muss man die äußeren Ableitung mit der inneren ableitung von \(cos(\omega\cdot t)\) multiplizieren.
Die äußeren Ableitung von \(cos(\omega t)\) lautet:
\(-sin(\omega\cdot t)\)
und die innere Ableitung lautet:
\(\frac{d(\omega\cdot t)}{dt}\)\(=\omega\)
Die innere Ableitung mal die äußere Ableitung liefert also:
\(v(t)=-x_0\cdot \omega\cdot sin(\omega t)\)
Wie sieht der zeitliche Verlauf der Geschwindigkeit für das Fadenpendel aus?
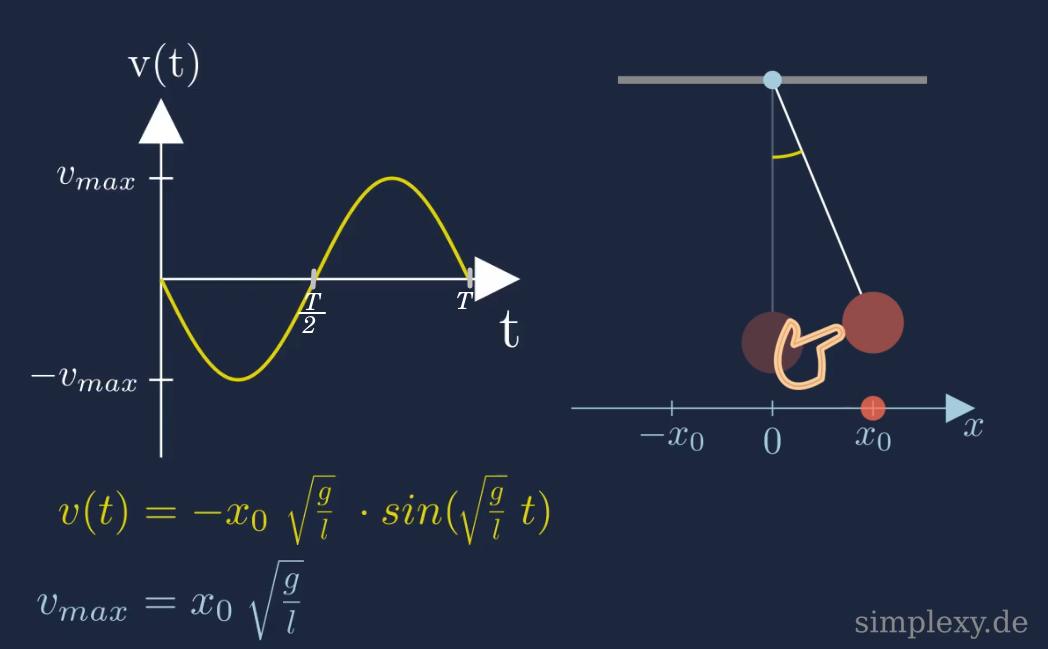
In der oberen Abbildung ist der zeitliche Verlauf der Geschwindigkeitsfunktion dargestellt. Zum Zeitpunkt \(t=0\) wurde das Pendel noch nicht losgelassen, daher ist die Geschwindigkeit gleich Null. Sobald das Fadenpendel losgelassen wird, beschleunigt es sich in Richtung der Ruhelage. Dabei nimmt die Geschwindigkeit zu. Beim Durchgang durch die Ruhelage, erreicht die Geschwindigkeit ein Maximum (im Graphen ein Minimum da eine Bewegung nach Links mit einer negativen Geschwindigkeit definiert ist). Anschließend schwingt das Pendel zum anderen Umkehrpunkt, während seine Geschwindigkeit abnimmt. Am Umkehrpunkt angekommen (\(t=\frac{T}{2}\)), ist die Geschwindigkeit schließlich auf Null gefallen. Nun wird das Pendel wieder in Richtung der Ruhlage beschleunigt. Die Geschwindigkeit nimmt wieder zu und erreicht erneut sein Maximum, beim Durchgang durch die Ruhlage. Aufgrund der Trägheit des Pendelkörpers, bewegt es sich weiter zum ersten Umkehrpunkt, wobei die Geschwindigkeit wieder abnimmt. Am Umkehrpunkt angekommen (\(t=T\)) ist die Geschwindigkeit wieder Null.
Merke
Die hier betrachtete Ort-Zeit-Funktion \(x(t)=x_0\cdot cos(\omega\cdot t)\), geht einher mit einem Fadenpendel das zum start Zeitpunkt \(t=0\) nach Rechts ausgelenkt ist (\(x_0\)). Man kann das Fadenpendel zum start Zeitpunkt in der Ruhelage lassen und dann nach rechts anstoßen. Die Ort-Zeit-Funktion wäre dann:
\(x(t)=x_0\cdot sin(\omega\cdot t)\)
und damit wäre die Geschwindigkeit für diesen Fall:
\(v(t)=x_0\cdot \omega\cdot cos(\omega t)\)
Die Ort-Zeit-Funktion und damit auch der zeitliche Verlauf der Geschwindigkeit ist von der Anfangsbedingung abhängig.
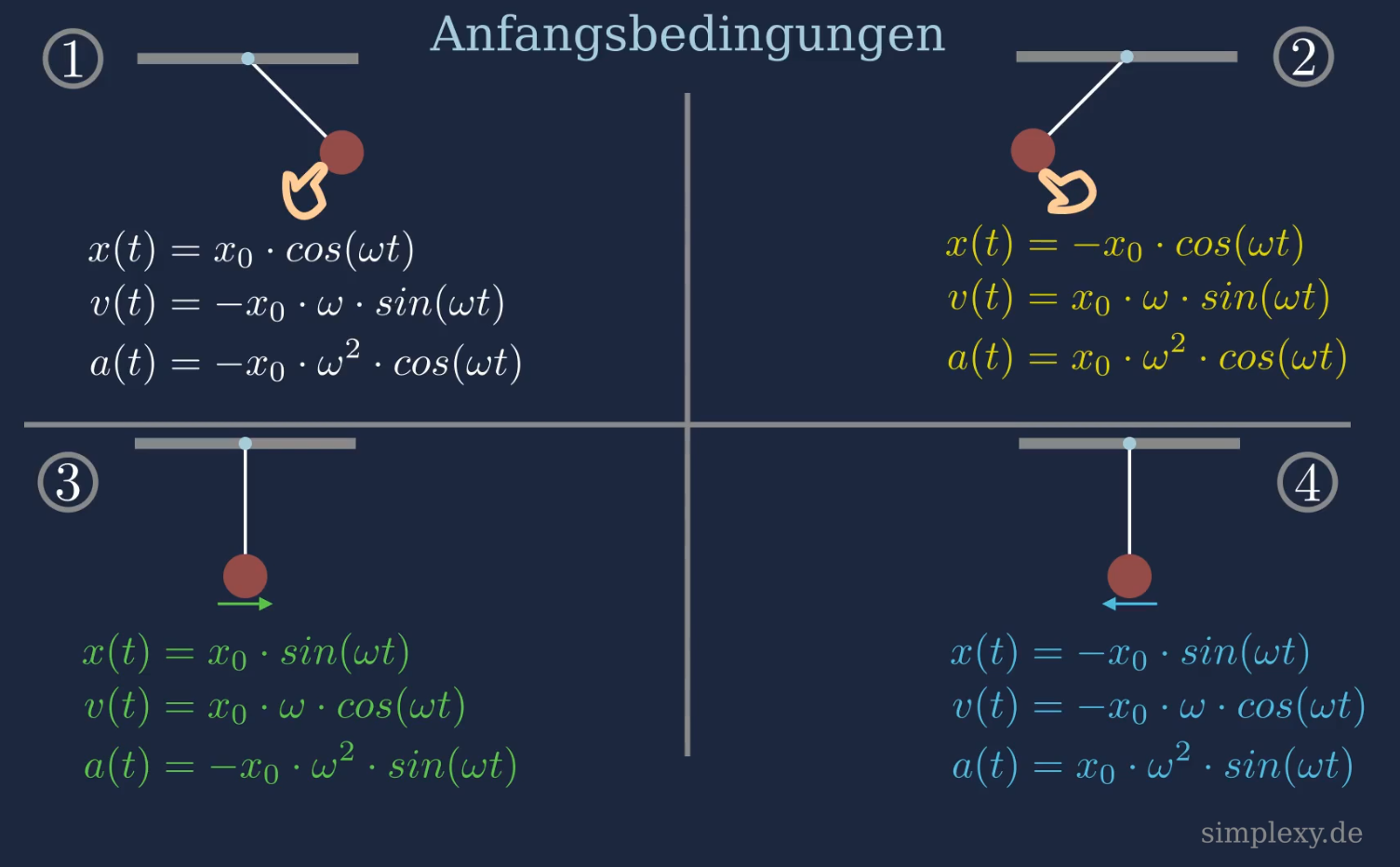
In der folgenden Abbildung ist die Ort-Zeit-Funktion, Geschwindigkeitsfunktion und die Beschleunigungsfunktion für verschiedene Anfangsbedingungen vom Fadenpendel angegeben.
Die Geschwindigkeit vom Fadenpendel ist im unteren Video leicht erklärt.
Fadenpendel Maximal Geschwindigkeit berechnen
Über den Energieerhaltungssatz kann man die höchste Geschwindigkeit vom Fadenpendel berechnen.
Energieerhaltungssatz beim Fadenpendel
Während der Schwingung des Fadenpendels bleibt die Gesamtenergie erhalten (bleibt konstant). Es findet jedoch fortwährend eine Umwandlung zwischen der kinetischen und der potentiellen Energie statt.
\(E_{ges}=E_{kin}+E_{pot}=konstant\)
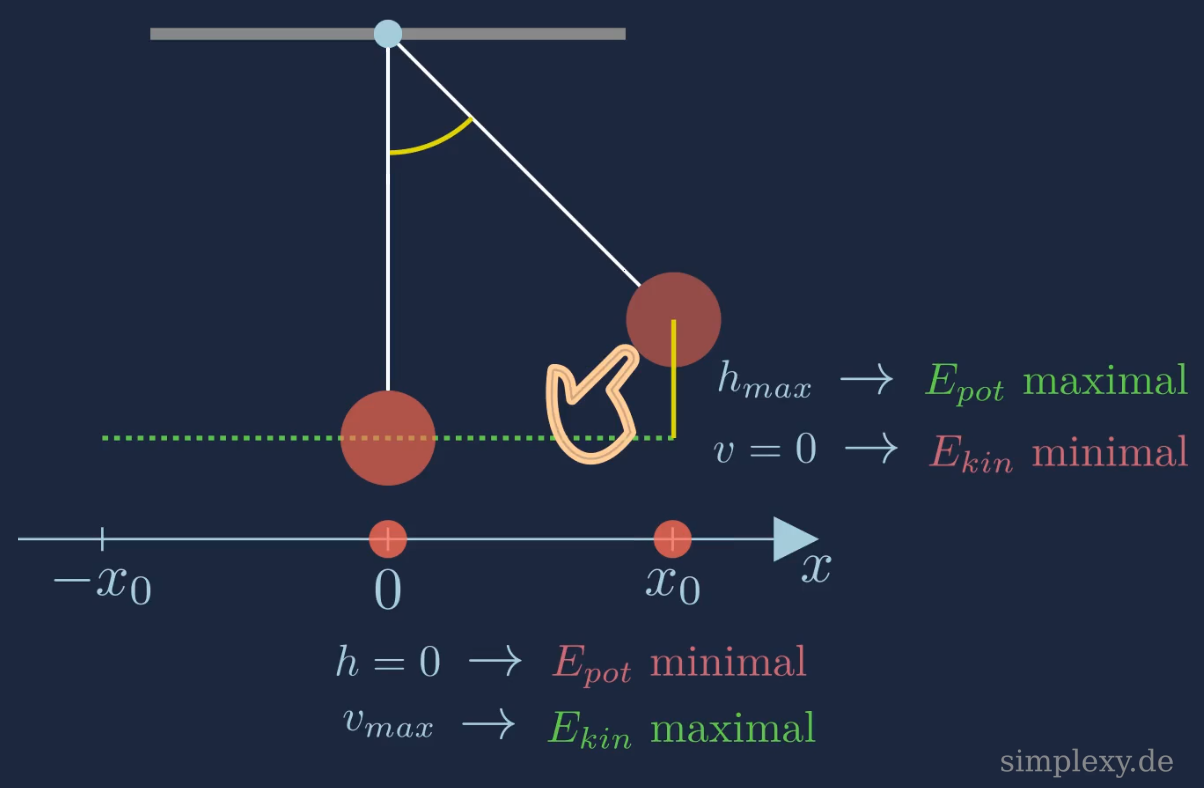
Die potentielle Energie (Lage bzw. Höhenenergie) ist an den Umkehrpunkten Maximal. Dort ist die Höhe des Pendels am größten. An den Umkehrpunkten steckt die Gesamtenergie des Pendel in der potentiellen Energie. Beim Durchgang durch die Ruhelage steckt die Gesamtenergie des Pendels in der kinetischen Energie (Bewegungsenergie). Wir können also beide Maximal-Energien gleichsetzen.
\(\begin{aligned} E_{kin,max}&=E_{pot,max}\\ \\ \frac{1}{2}\cdot m\cdot v_{max}^2&=m\cdot g\cdot h_{max}\\ \end{aligned}\)
Diese Gleichung kann nun nach der maximalen Geschwindigkeit des Fadenpendels umgestellt werden.
\(\begin{aligned} \frac{1}{2}\cdot m\cdot v_{max}^2&=m\cdot g\cdot h_{max}\,\,\,|\cdot 2\\ \\ m\cdot v_{max}^2&=2\cdot m\cdot g\cdot h_{max}\,\,\,|\div m\\ \\ v_{max}^2&=2\cdot g\cdot h_{max}\,\,\,|\sqrt{\,\,\,}\\ \\ v_{max}&=\sqrt{2\cdot g\cdot h_{max}} \end{aligned}\)
Ist die Höhe \(h_{max}\) bekannt, so kann man die maximale Geschwindigkeit vom Fadenpendel berechnen.
Maximale Geschwindigkeit
\(\begin{aligned} v_{max}&=\sqrt{2\cdot g\cdot h_{max}} \end{aligned}\)
