Schwingungsdauer und Amplitude
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Pendel Schwingung
Für jedes Schwingungsfähiges System lässt sich eine Schwingungsdauer und eine Amplitude berechnen oder ermitteln. In diesem Beitrag wird vorallem auf die Schwingung vom Fadenpendel und Federpendel eingegangen. Um die harmonische Schwingung vom Fadenpendel in kurzer Zeit zu verstehen, kannst du dir das Video zum Fadenpendel ansehen. Ähnliche Videos für das Federpendel haben wir ebenfalls für dich bereitgestellt.
Amplitude
Die Amplitude ist die betragsmäßig größte Auslenkung eines Pendels. Im allgemeinen wird die Amplitude mit dem Formelzeichen \(A\) angegeben.
Die allgemeine Ort-Zeit-Funktion \(s(t)\) einer ungedämpften harmonischen Schwingung lautet:
\(\begin{aligned} s(t)=A\cdot cos(\omega\cdot t) \end{aligned}\)
wobei \(A\) die Amplitude und \(\omega\) die Kreisfrequenz der Schwingung ist.
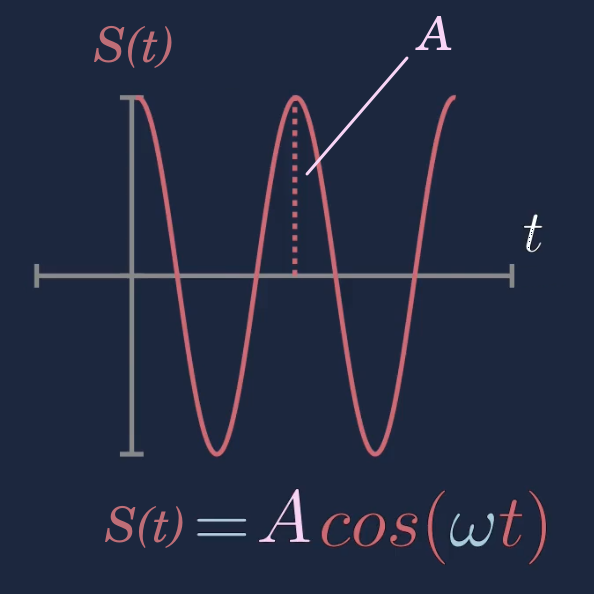
Die Amplitude \(A\) ist stets als positive Zahl definiert. Die Auslenkung eines Pendels kann hingegen sowohl positiv als auch negativ sein. Die Auslenkung bezeichnet den Abstand eines Pendelkörpers von seiner Ruheposition (Ruhelage). Während der Schwingung eines Pendels, ändert sich die Auslenkung mit der Zeit. Daher wird die Auslenkung über eine Ort-Zeit-Funktion beschrieben. In der Ort-Zeit-Funktion taucht die Amplitude \(A\) auf. Sie gibt die betragsmäßig größte Auslenkung des Pendelkörpers an. Bei einer ungedämpften harmonischen Schwingung ist die Amplitude \(A\) immer gleich groß (konstant). Sie ändert sich also im gegensatz zu der Auslenkung nicht. Betrachtet man jedoch eine gedämpfte Schwingung, so ist auch die Amplitude Zeit abhängig. Sie nimmt dann im laufe der Zeit ab.
In der unteren Abbildung ist die Ort-Zeit-Funktion einer ungedämpften und einer gedämpften Schwingung dargestellt.
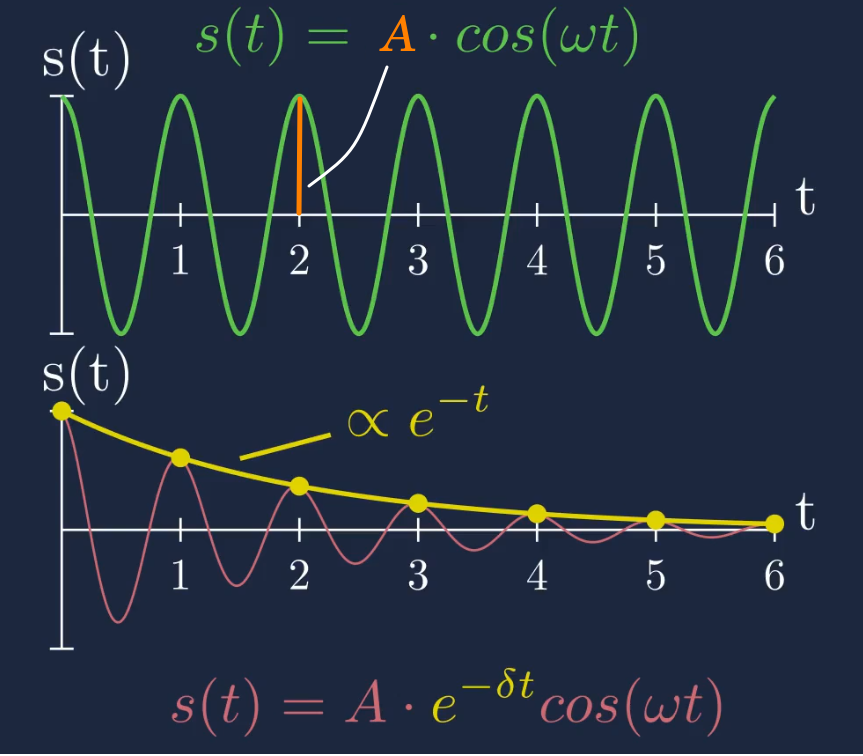
Amplitude
-
Die Amplitude ist die betragsmäßig größte Auslenkung eines schwingungsfähigen Systems.
-
Die Amplitude ist als positive Zahl definiert.
-
Bei einer ungedämpften Schwingung ist die Amplitude konstant.
-
Bei einer gedämpften Schwingung nimmt die Amplitude mit der Zeit ab.
Amplitude berechnen
Die Ort-Zeit-Funktion einer harmonischen Schwingung lautet:
\(\begin{aligned} s(t)=A\cdot cos(\omega\cdot t) \end{aligned}\)
Die Ort-Zeit-Funktion beschreibt das zeitliche verhalten der Auslenkung in Abhängigkeit von der Zeit. Dabei ist der \(cos(\omega\cdot t)\) Term für die Schwingung des pendels mit einer gewissen Kreisfrequenz \(\omega\) zuständig und \(A\) gibt die Amplitude wieder. Die Amplitude \(A\) wird bei der ersten Auslenkung des Pendel vorgegeben.
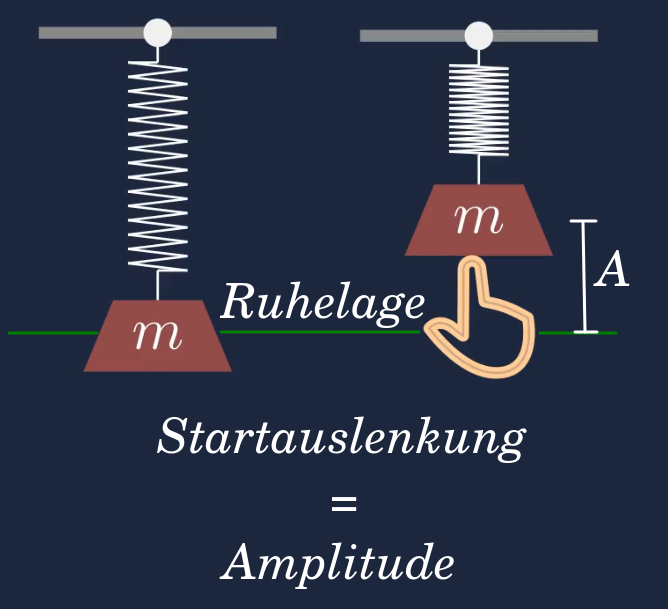
Betrachtet man ein ungedämpftes Federpendel, das zu Beginn um eine gewisse Strecke aus der Ruhelage nach Oben ausgelenkt wird, so entspricht der Abstand um den man das Pendel aus der Ruhelage auslenkt die Amplitude. Die Amplitude der Schwingung ist gleich der Startauslenkung.
Wird hingegen ein Fadenpendel betrachtet, dass zu Beginn um die Strecke \(s_0\) nach rechts aus der Ruhelage auslenkt wird, so entspricht die Amplitude \(A\) gerade die Startauslenkung \(s_0\).
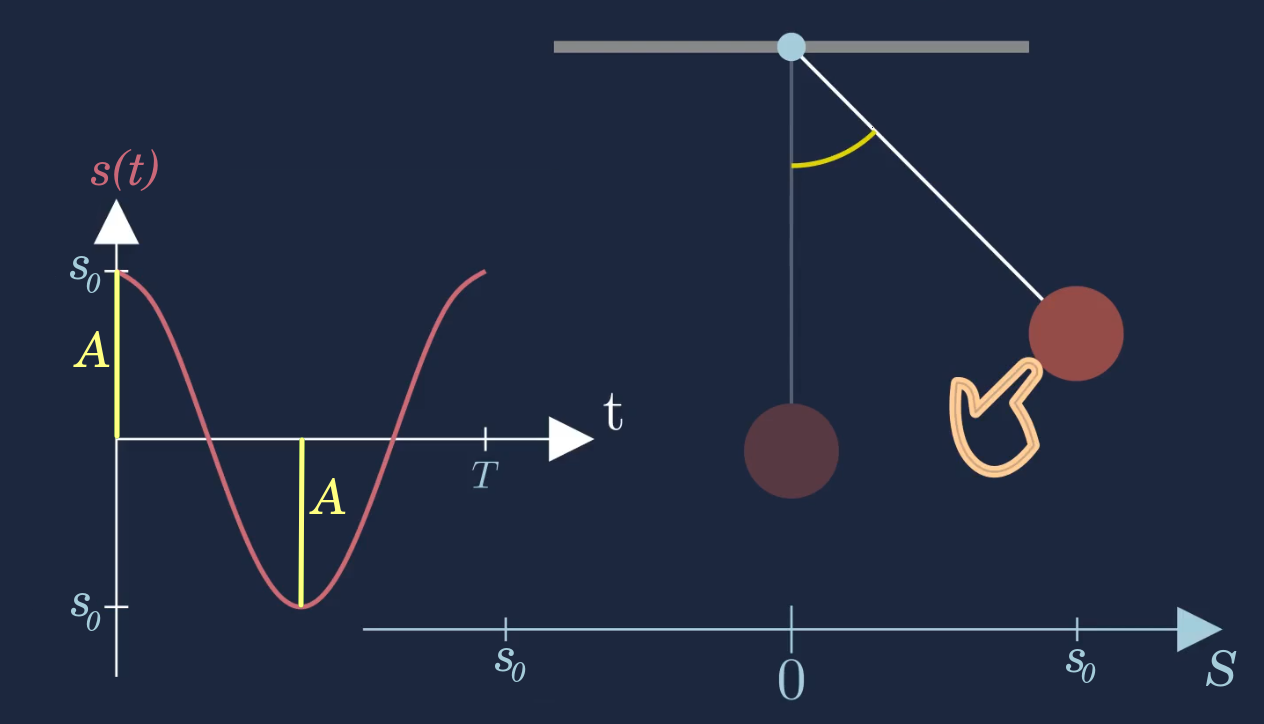
Schwingungsdauer und Periodendauer
Die Schwingungsdauer ist die Zeit, die ein schwingungsfähiges System benötigt um einen Schwingungsvorgang zu vollführen. Die Schwingungsdauer wird oftmals auch als Periodendauer bezeichnet. Ein vollständiger Schwingungsvorgang ist vollführt, wenn der Pendelkörper eine "Hin- und Her-Bewegung" durchgeführt hat. Sprich, von einem Umkehrpunkt zum anderen Umkehrpunkt und wieder zurück zum ersten Umkehrpunkt.
Schwingungsdauer
-
Die Zeit für einen Schwingungsvorgang wird Schwingungsdauer oder Periodendauer genannt.
-
Die Schwingungsdauer hat das Formelzeichen \(T\).
-
Die Einheit der Schwingungsdauer ist Sekunde \([s]\).
Schwingungsdauer berechnen
Um die Schwingungsdauer berechnen zu können, benötigt man den Zusammenhang zur Kreisfrequenz.
Schwingungsdauer Formel
\(\begin{aligned} T=\frac{2\pi}{\omega} \end{aligned}\)
Die Kreisfrequenz \(\omega\) ist je nach Pendel unterschiedlich definiert. Wir werden uns im folgenden mit der Schwingungsdauer für das Fadenpendel und Federpendel beschäftigen.
Schwingungsdauer Federpendel
Die Schwingungsgleichung für das Federpendel lautet:
\(\begin{aligned} \ddot{s}(t)+\frac{D}{m}s(t)=0 \end{aligned}\)
dabei ist \(s(t)\) die Auslenkung des Pendels aus der Ruhelage, \(D\) die Federkonstante und \(m\) die Masse des Pendelkörpers.
Die Lösung dieser Schwingungsgleichung lautet:
\(\begin{aligned} s(t)=A\cdot cos(\omega\cdot t) \end{aligned}\)
wobei \(A\) die Amplitude und \(\omega\) die Kreisfrequenz der harmonischen Schwingung ist. Sie ist gegeben über:
\(\begin{aligned} \omega=\sqrt{\frac{D}{m}} \end{aligned}\)
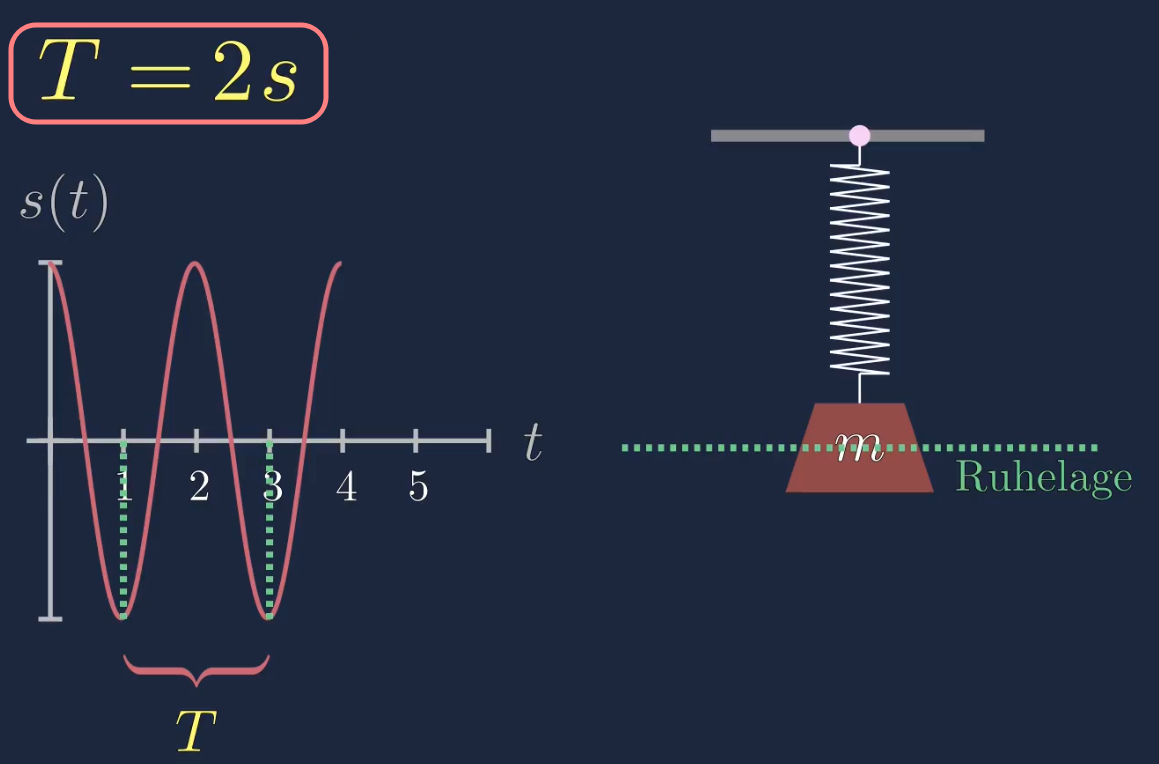
Nutzt man nun den Zusammenhang zwischen der Schwingungsdauer und der Kreisfrequenz, so folgt für die Schwingungsdauer vom Federpendel:
\(\begin{aligned} T&=\frac{2\pi}{\omega}\\ \\ T&=2\pi\cdot\sqrt{\frac{m}{D}} \end{aligned}\)
Schwingungsdauer Federpendel
Die Schwingungsdauer vom Federpendel gibt an, wie lange eine vollständige Periode der harmonischen Schwingung dauert.
\(\begin{aligned} T&=2\pi\cdot\sqrt{\frac{m}{D}} \end{aligned}\)
Wie ist der Zusammenhang zwischen der Schwingungsdauer und der Masse?
Vergrößert man die Masse \(m\), so wird die Schwingungsdauer größer. Das Pendel schwingt also langsamer.
Verkleinert man die Masse \(m\), so wird die Schwingungsdauer kleiner. Das Pendel schwingt also schneller.
Wie ist der Zusammenhang zwischen der Schwingungsdauer und der Federkonstant?
Vergrößert man die Federkonstant \(D\), so wird die Schwingungsdauer kleiner. Das Pendel schwingt also schneller.
Verkleinert man die Federkonstant \(D\), so wird die Schwingungsdauer größer. Das Pendel schwingt also langsamer.
Schwingungsdauer Fadenpendel
Die Schwingungsgleichung für das Fadenpendel lautet:
\(\begin{aligned} \ddot{x}(t)+\frac{g}{l}x(t)=0 \end{aligned}\)
dabei ist \(x(t)\) die Auslenkung des Pendels aus der Ruhelage, \(g\) die Fallbeschleunigung und \(l\) die Länge des Fadens. Eine Herleitung dieser Schwingungsgleichung kann du dir hier ansehen.
Die Lösung der Schwingungsgleichung lautet:
\(\begin{aligned} x(t)=x_0\cdot cos(\omega\cdot t) \end{aligned}\)
wobei \(x_0\) die Amplitude und \(\omega\) die Kreisfrequenz der harmonischen Schwingung ist. Sie ist definiert als:
\(\begin{aligned} \omega=\sqrt{\frac{g}{l}} \end{aligned}\)
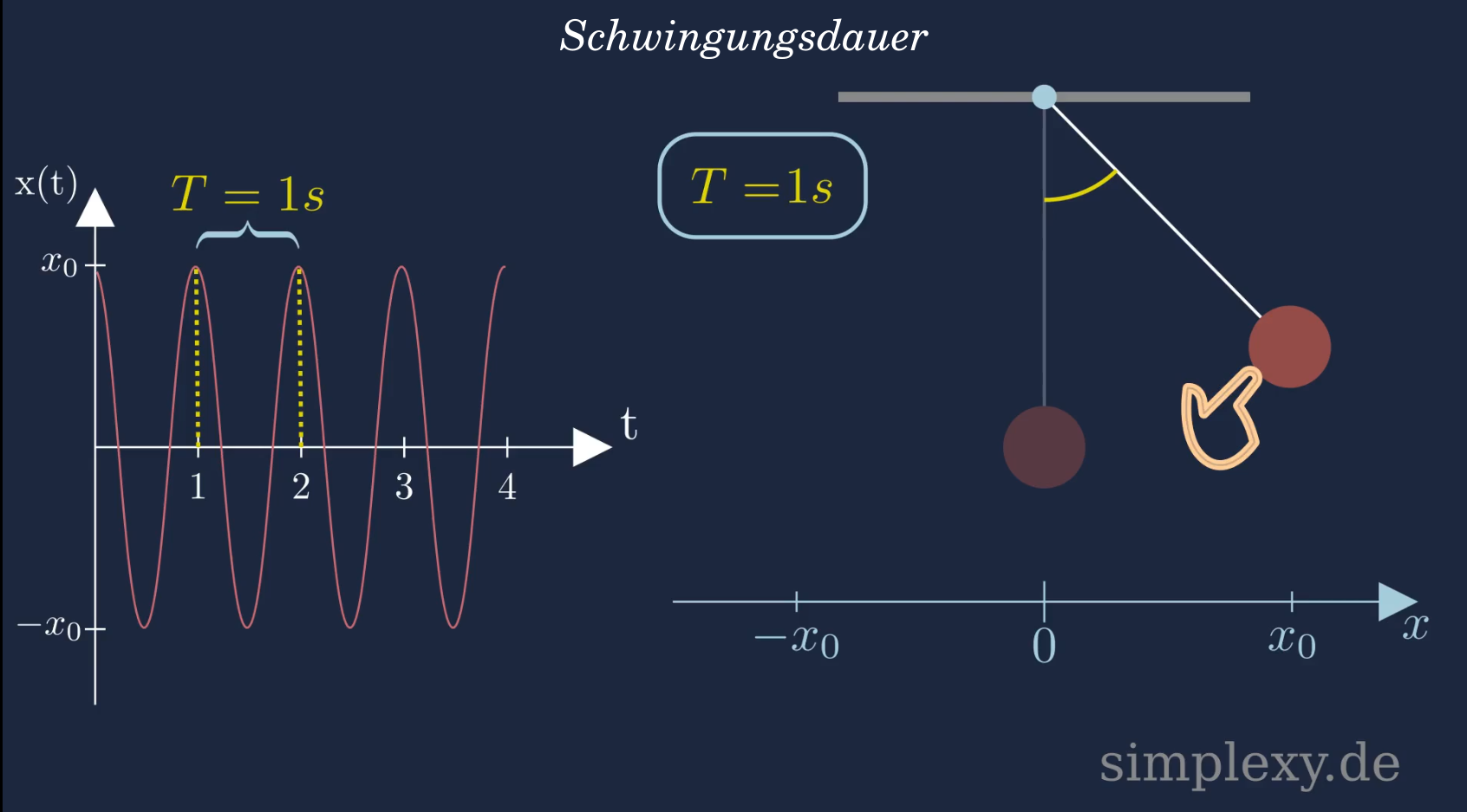
Verwendet man nun den Zusammenhang zwischen der Schwingungsdauer und der Kreisfrequenz vom Fadenpendel, so folgt:
\(\begin{aligned} T&=\frac{2\pi}{\omega}\\ \\ T&=2\pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
Schwingungsdauer Federpendel
Die Schwingungsdauer vom Fadenpendel gibt an, wie lange eine vollständige Periode der harmonischen Schwingung dauert.
\(\begin{aligned} T&=2\pi\cdot\sqrt{\frac{l}{g}} \end{aligned}\)
Wie ist der Zusammenhang zwischen der Schwingungsdauer und der Länge des Fadens?
Vergrößert man die Länge \(l\), so wird die Schwingungsdauer größer. Das Pendel schwingt also langsamer.
Verkleinert man die Länge \(l\), so wird die Schwingungsdauer kleiner. Das Pendel schwingt also schneller.
Wie ist der Zusammenhang zwischen der Schwingungsdauer und der Fallbeschleunigung?
Vergrößert man die Fallbeschleunigung \(g\), so wird die Schwingungsdauer kleiner. Das Pendel schwingt also schneller.
Verkleinert man die Fallbeschleunigung \(g\), so wird die Schwingungsdauer größer. Das Pendel schwingt also langsamer.
-
Die Schwingungsdauer des Fadenpendels ist von Masse \(m\) des Pendelkörpers unabhängig.
-
Findet die Schwingung des Fadenpendels auf der Erde statt, so ist die Fallbeschleunigung \(g=9,81\frac{m}{s^2}\) konstant. Die Schwingungsdauer ist somit nur noch von der Länge \(l\) des Fadens abhängig.
Schwingungsdauer und Frequenz
Die Frequenz gibt an, wie viele Perioden innerhalb einer Sekunde stattfinden. Sie wird durch ein \(f\) symbolisiert und hat die Einheit \([\frac{1}{s}=Hz]\) (Hertz). Man kann die Frequenz berechnen indem man den Kehrwert der Schwingungsdauer bestimmt.
Frequenz
Die Frequenz gibt die Anzahl an Schwingungen an, die ein Pendel innerhalb einer Sekunde vollführt.
\(\begin{aligned} f=\frac{1}{T} \end{aligned}\)
