Federpendel Energieformen
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Das Wichtige zusammengefasst
Die Schwingungsgleichung eines Federpendels kann man aus dem Hookeschen Gesetzt ableiten.
Die Schwingungsgleichung lautet:
\(m\cdot \frac{d^2s}{dt^2}+D\cdot s=0\)
Dabei ist:
\(m\) die Masse,
\(s\) die Auslenkung,
und \(D\) die Federkonstante des Pendels.
Das Federpendel schwingt harmonisch mit der Zeit-Ort-Funktion
\(s(t)=A\cdot cos(\omega t)\)
Dabei ist \(\omega\) die Eigenfrequenz bzw. Kreisfrequenz des Pendels.
\(A\) ist die Startauslenkung (Amplitude) des Pendels.
\(\omega=\sqrt{\frac{D}{m}}\)
Die potentielle Energie eines Federpendels berechnet sich über die Verformungsenergie der Feder und lautet:
Die kinetische Energie berechnet sich über \(E_{kin}=\frac{1}{2}m\cdot v^2\) und lautet lautet:
\(E_{pot}=\frac{1}{2}D\cdot s(t)^2\)
\(E_{pot}=\frac{1}{2}D\cdot A^2\cdot cos^2(\omega\cdot t)\)
\(E_{kin}=\frac{1}{2}m\cdot \dot{s}(t)^2\)
\(E_{kin}=\frac{1}{2}m\cdot\omega^2\cdot A^2\cdot sin^2(\omega\cdot t)\)
Das Federpendel
Ein Federpendel besteht aus einer Schraubenfeder an dessen Ende eine Masse befestigt ist, welches sich gradlinig entlang der Auslenkungsrichtung bewegen kann. Während der Bewegung des Pendels verkürzt und verlängert sich die Feder periodisch, die Masse vollführt dabei eine harmonische Bewegung. Man nennt ein Federpendel unter anderem auch harmonischer Ozillator.
Betrachtet wird ein Federpendel, dass um die Streck \(s\) aus der Ruhelage ausgelengt ist.
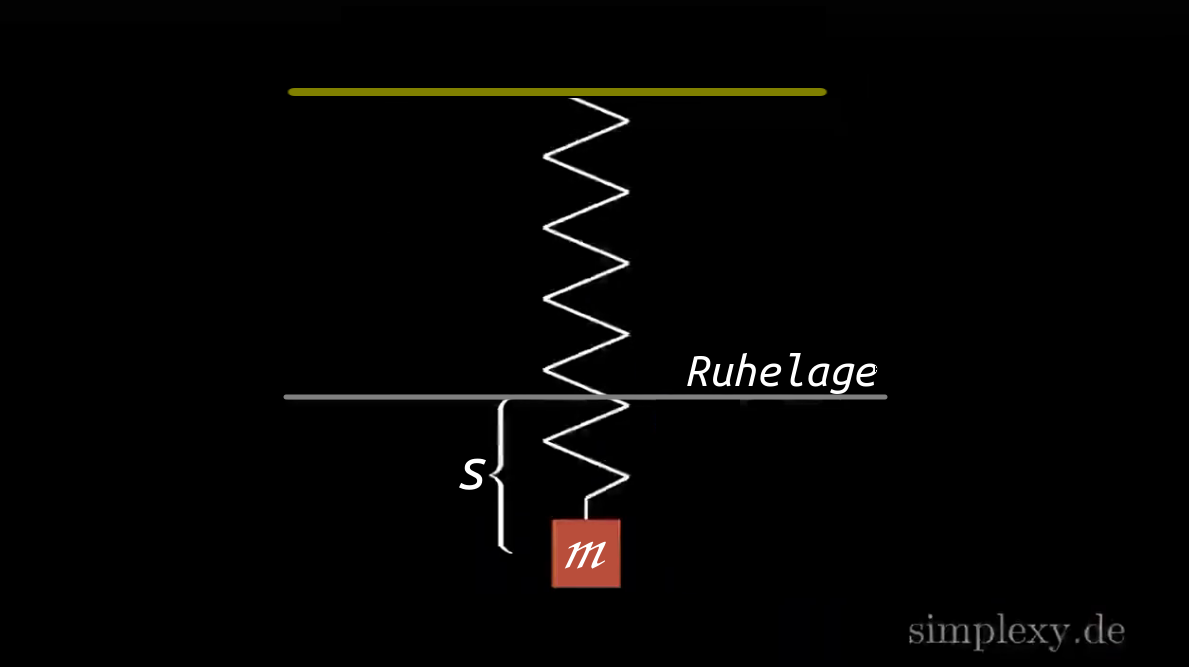
Spannernergie & Spannarbeit
Das Federpendel wird von der Ruhelage aus nach unten gezogen, dabei leistet man an der Feder Spannarbeit.
Die Spannarbeit bzw Verformungsarbeit ist eine Form der mechanischen Arbeit. Wird ein Körper verformt, so wird Verformungsarbeit verrichtet.
Spannarbeit einer Feder
\(W=\frac{1}{2}\cdot D\cdot s^2\)
Wobei gilt:
\(W\) ist die Verformungsarbeit bzw. Spannarbeit in Newton-Meter \([Nm]\)
\(s\) ist die Auslenkung bzw. die Dehnung der Feder in Meter \([m]\)
\(D\) ist die Federkonstante in Newton pro Meter \([\frac{N}{m}]\)
Aus dem Beitrag über das Hookesche Gesetz wissen wir, wie man die Kraft mit der eine Feder ausglenkt wurde berechnet
\(F=D\cdot s\)
Damit können wir die Spannarbeit einer Feder auch folgendermaßen ausdrucken:
\(W=\frac{1}{2}F\cdot s\)
Die potentielle Energie eines Federpenels ist genauso groß wie die geleistete Spannarbeit.
Potentielle Energie eines Federpendels
\(E_{pot}=\frac{1}{2}D\cdot s^2\)
bzw.
\(E_{pot}=\frac{1}{2}F\cdot s\)
An den Umkehrpunkten ist die potentielle Energie maximal. An den Punkten wo die Auslenkung maximal ist, nimmt die potentielle Energie also ihren maximalen Wert an. An den Umkehrpunkten ist die Geschwindigkeit des Pendels für einen kurzen Augenblick Null \((v=0)\).
Da das Pendel im Laufe der Zeit seine Auslenkung ändert, ändert sich im laufe der Zeit auch die potentielle Energie des Pendels. Um den Verlauf der potentiellen Energie zu erhalten können wir die Lösung der Bewegungsgleichung in die Formel für die potentielle Energie einsetzen. In dem Beitrag über das Federpendel haben wir die Lösung \(s(t)\) der Bewegungsgleichung berechnet:
\(s(t)=A\cdot cos(\omega\cdot t)\)
Einsetzen in die Formel für die potentielle Energie liefert:
\(E_{pot}=\frac{1}{2}D\cdot A^2\cdot cos^2(\omega\cdot t)\)
Mit \(\omega=\sqrt{\frac{D}{m}}\)
Für den Fall
\(A=1\), \(D=1\), \(m=1\)
sehe der Graph für die potentielle Energie wie folgt aus:
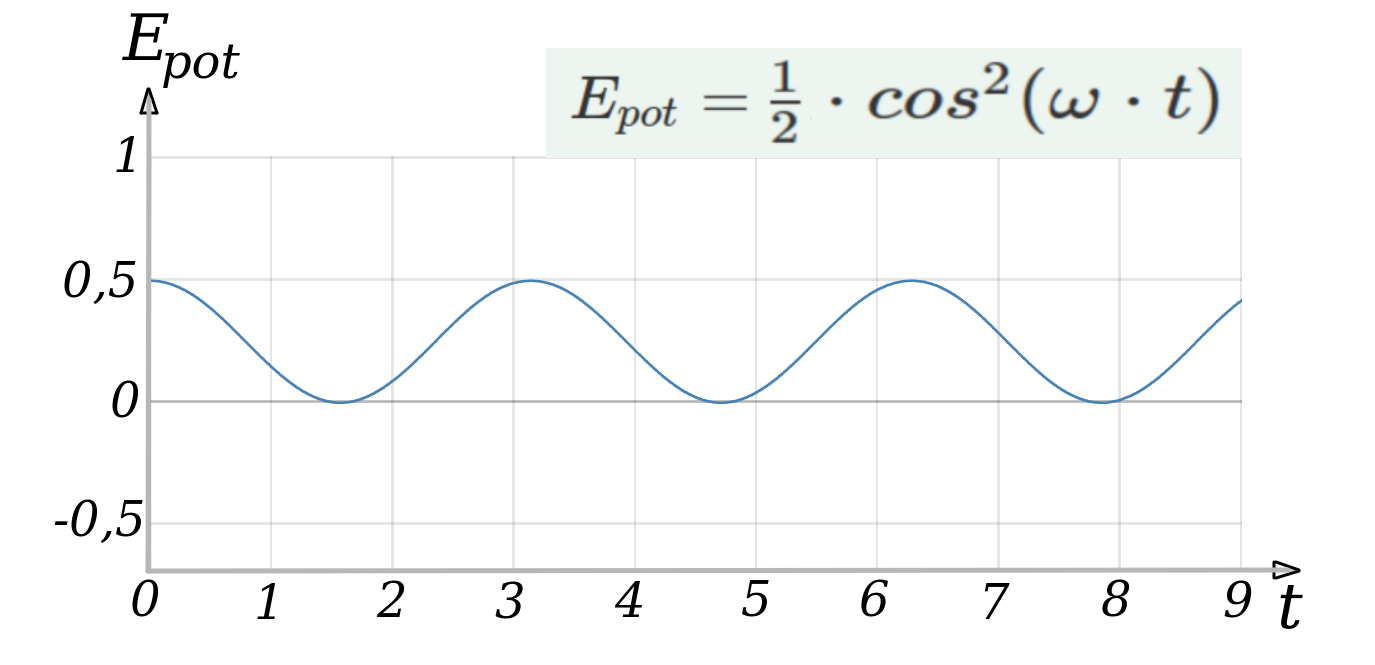
Kinetische Energie
Wird das Federpendel losgelassen, so wird es sich in Richtung der Ruhelage beschleunigen. Aufgrund der Trägheit der Masse kommt das Pendel am Ruhepunkt nicht zum Stillstand, es bewegt sich weiter bis zum nächsten Umkehrpunkt wo das Pendel für einen kurzen moment die Geschwindigkeit \(v=0\) besitzt. Im Anschluss wird das Pendel wieder zurück in Richtung der Ruhelage beschleunigt. Während der Bewegung des Pendels kommt es zu einer Umwandlung zwischen der potentiellen und der kintetischen Energie des Pendels.
Kinetische Energie
\(E_{kin}=\frac{1}{2}m\cdot v^2\)
Die kinetische Energie eines Körpers ist von dessen Geschwindigkeit abhängig. Um die Geschwindigkeit des Pendel zu ermitteln, können wir die Lösung \(s(t)\) der Bewegungsgleichung nach der Zeit ableiten.
\(v(t)=\dot{s}(t)\)
\(v(t)=-\omega\cdot A\cdot sin(\omega t)\)
Wir können die Formel für die Geschwindigkeit in die Formel für die kinetische Energie einsetzen:
Kinetische Energie eines Federpendels
\(E_{kin}=\frac{1}{2}m\cdot\omega^2\cdot A^2\cdot sin^2(\omega\cdot t)\)
Wenn man \(\omega=\sqrt{\frac{D}{m}}\) in die Formel für die kinetische Energie des Federpendels einsetzt, dann erhält man:
\(E_{kin}=\frac{1}{2}m\cdot\sqrt{\frac{D}{m}}^2\cdot A^2\cdot sin^2(\sqrt{\frac{D}{m}}\cdot t)\)
\(E_{kin}=\frac{1}{2}\cdot D\cdot A^2\cdot sin^2(\sqrt{\frac{D}{m}}\cdot t)\)
Für den Fall \(D=0\), \(A=0\) und \(m=0\) sieht der Graph für die kinetische Energie wie folgt aus:
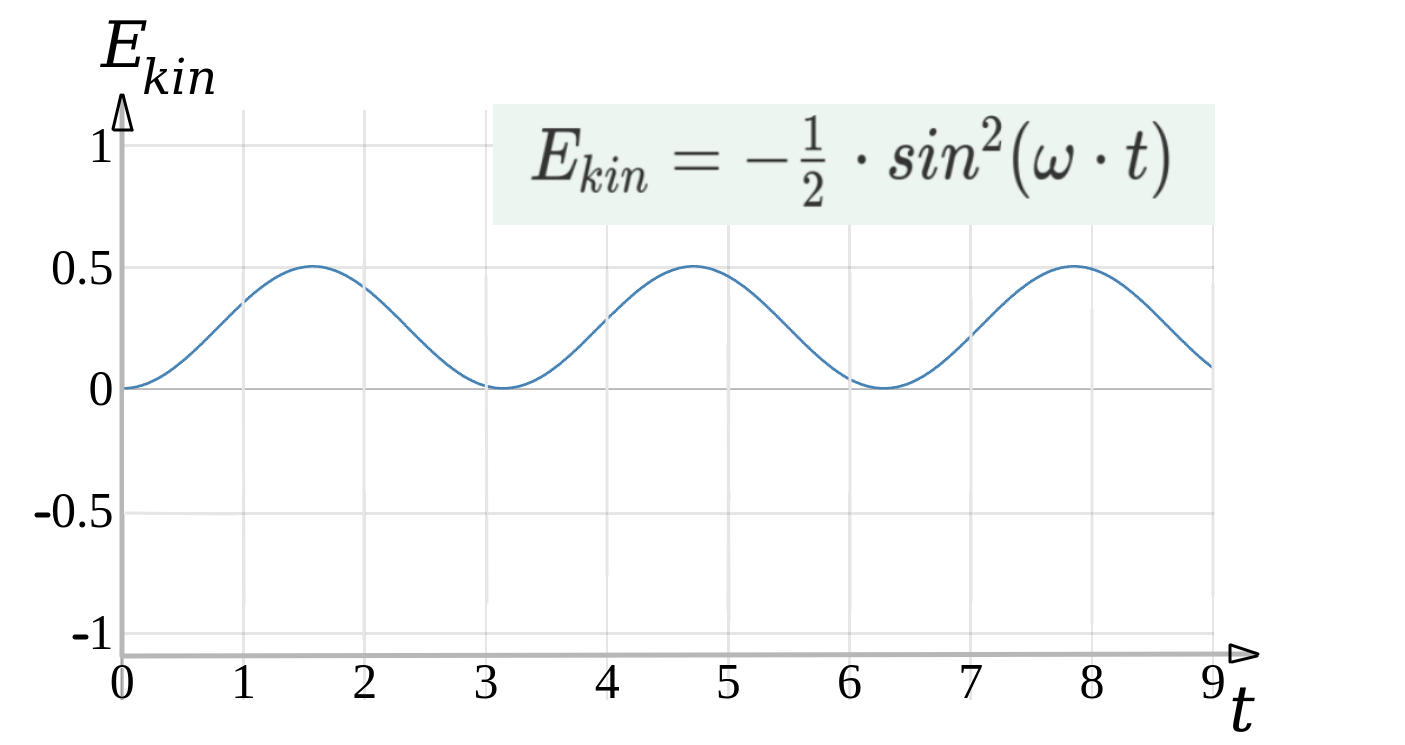
Das Federpendel bestizt an den Umkehrpunkten für einen kurzen moment die Geschwindigkeit \(v=0\), an den Umkehrpunkten ist die kinetische Energie des Pendels Null. Die Feder ist an den Umkehrpunkten maximal gedehnt bzw. gestaucht und bestizt damit die höchste Verformungsenergie bzw. potentielle Energie.
Beim Durchgang durch die Ruhelage ist die Geschwindigkeit maximal und damit die kinetische Energie maximal. In der Ruhelage ist die Feder nicht verformt und die potentielle Energie ist Null. Es findet eine permanente Umwandung zwischen der potentiellen und der kinetischen Energie statt.
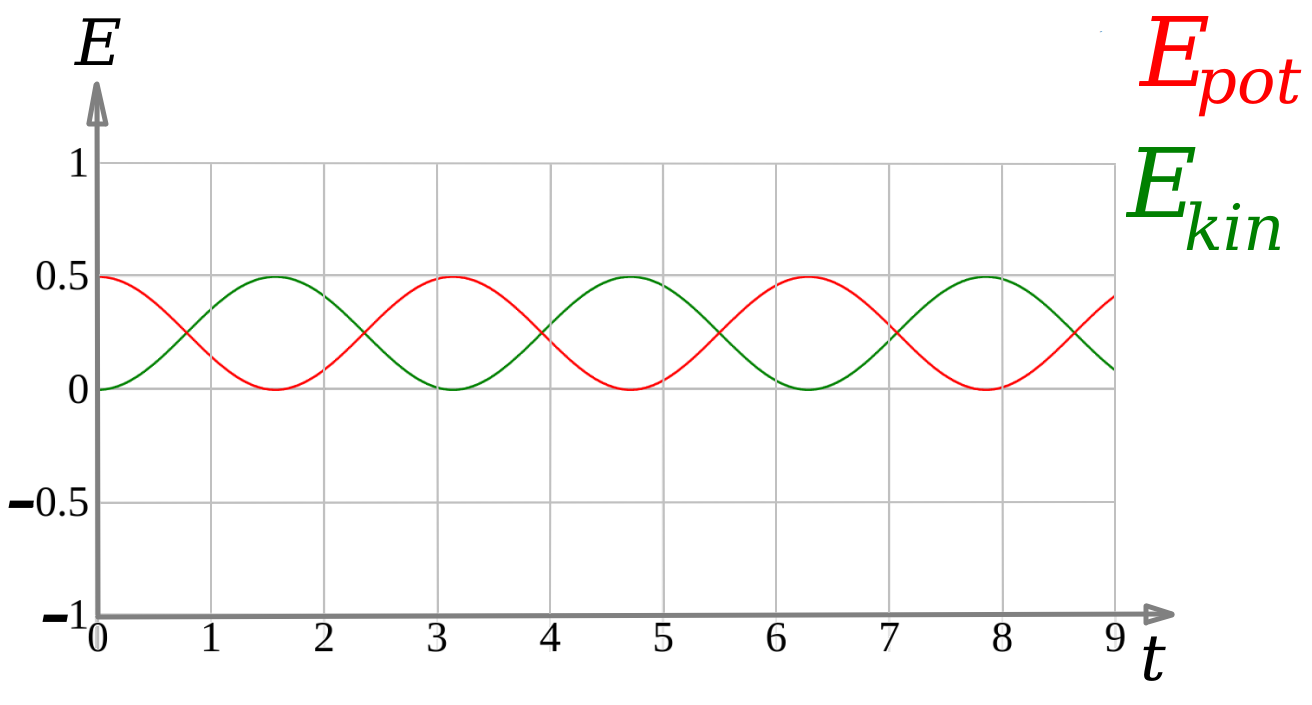
Gesamtenergie
Die Gesamtenergie ist die Summe aus der potentiellen und der kinetischen Enegie.
\(E_{ges}=E_{pot}+E_{kin}\)
\(E_{ges}=\frac{1}{2}D\cdot A^2\cdot cos^2(\omega\cdot t)+\frac{1}{2}\cdot D\cdot A^2\cdot sin^2(\omega\cdot t)\)
\(E_{ges}=\frac{1}{2}D\cdot A^2\Big(\underbrace{cos^2(\omega\cdot t)+sin^2(\omega\cdot t)}_{=1}\Big)\)
\(E_{ges}=\frac{1}{2}D\cdot A^2\)
Gesamtenergie
\(E_{ges}=E_{pot}+E_{kin}\)
\(E_{ges}=\frac{1}{2}D\cdot A^2\)
Ist die Federkonstante \(D\) unbekannt, dafür aber die Eigenfrequenz \(\omega\) gegeben, so kann die Gesamtenergie geschrieben werden als:
\(E_{ges}=\frac{1}{2}\omega^2\cdot m\cdot A^2\)
Dabei haben wir die Formel \(\omega^2=\frac{D}{m}\) nach \(D\) umgestellt und in die Formel für die Gesamtenergie eingestezt.
\(D=\omega^2\cdot m\)
Vernachlässigt man jede Form von Reibung, dann bleibt die Gesamtenergie während der Schwingung des Pendels konstant. Es findet lediglich eine Umwandlung zwischen der kinetischen und der potentiellen Energie statt.
Energieerhaltung
\(E_{ges}=konstant\)
