Bahngeschwindigkeit vektoriell
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Bahngeschwindigkeit Vektor
Bewegt sich ein Körper entlang einer Kreisbahn mit festem Radius, so vollführt er eine Kreisbewegung. Die Bahngeschwindigkeit einer Kreisbewegung haben wir bereits in diesem Beitrag behandelt. Dort haben wir jedoch nur den Betrag der Bahngeschwindigkeit betrachtet. In diesem Beitrag hingegen wird der Vektor der Bahngeschwindigkeit betrachtet.
Bahngeschwindigkeit Formel
Wir wissen bereits, dass der Betrag der Bahngeschwindigkeit über die folgende Formel berechnet werden kann:
\(\begin{aligned} v=\frac{2\pi r}{T} \end{aligned}\)
Dabei ist \(r\) der Radius der Kreisbahn und \(T\) die Umlaufdauer.
Die Bahngeschwindigkeit kann auch über die Winkelgeschwindigkeit \(\omega\) ausgedrückt werden:
\(\begin{aligned} v=r\cdot \omega \end{aligned}\)
Bahngeschwindigkeit Vektoriell
In der Translationsbewegung ist die Geschwindigkeit eine vektorielle Größe, das gleiche gilt auch für die Bahngeschwindigkeit in der Kreisbewegung. Die Bahngeschwindigkeit besitzt eine Richtung und einen Betrag. In einer Kreisbewegung ist die Bahngeschwindigkeit immer tangential zur Kreisbahn gerichtet.
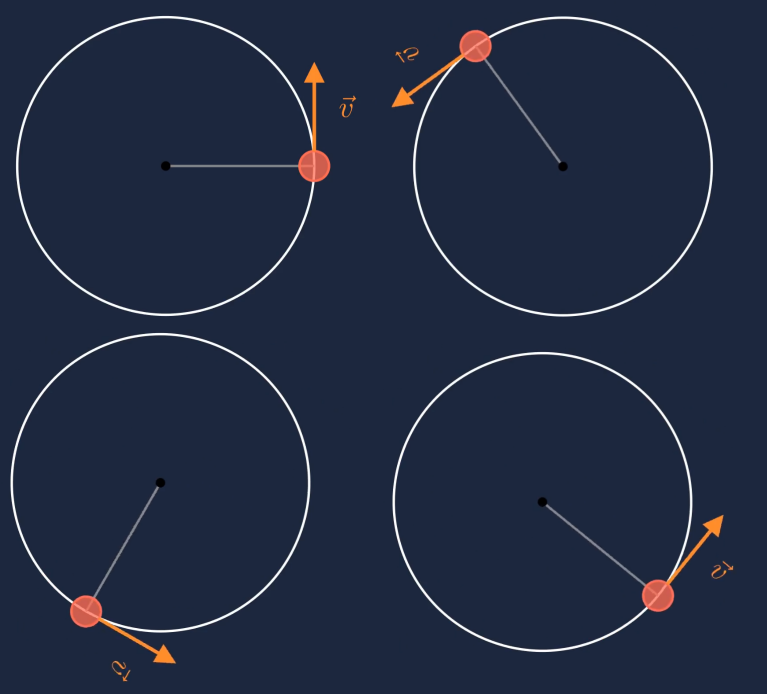
Ist die Länge des Vektors der Bahngeschwindigkeit zu jedem Zeitpunkt gleich groß, so ist der Betrag der Bahngeschwindigkeit konstant. Es handelt sich dann um eine gleichförmige Kreisbewegung. Die Richtung vom Vektor der Bahngeschwindigkeit ändert sich jedoch stets.
Bahngeschwindigkeit Vektor
Bei einer gleichförmigen Kreisbewegung ist der Vektor der Bahngeschwindigkeit tangential zur Kreisbahn bzw. senkrecht zum Radiusvektor. Der Betrag der Bahngeschwindigkeit berechnet sich über:
\(\begin{aligned} v=r\cdot \omega \end{aligned}\)
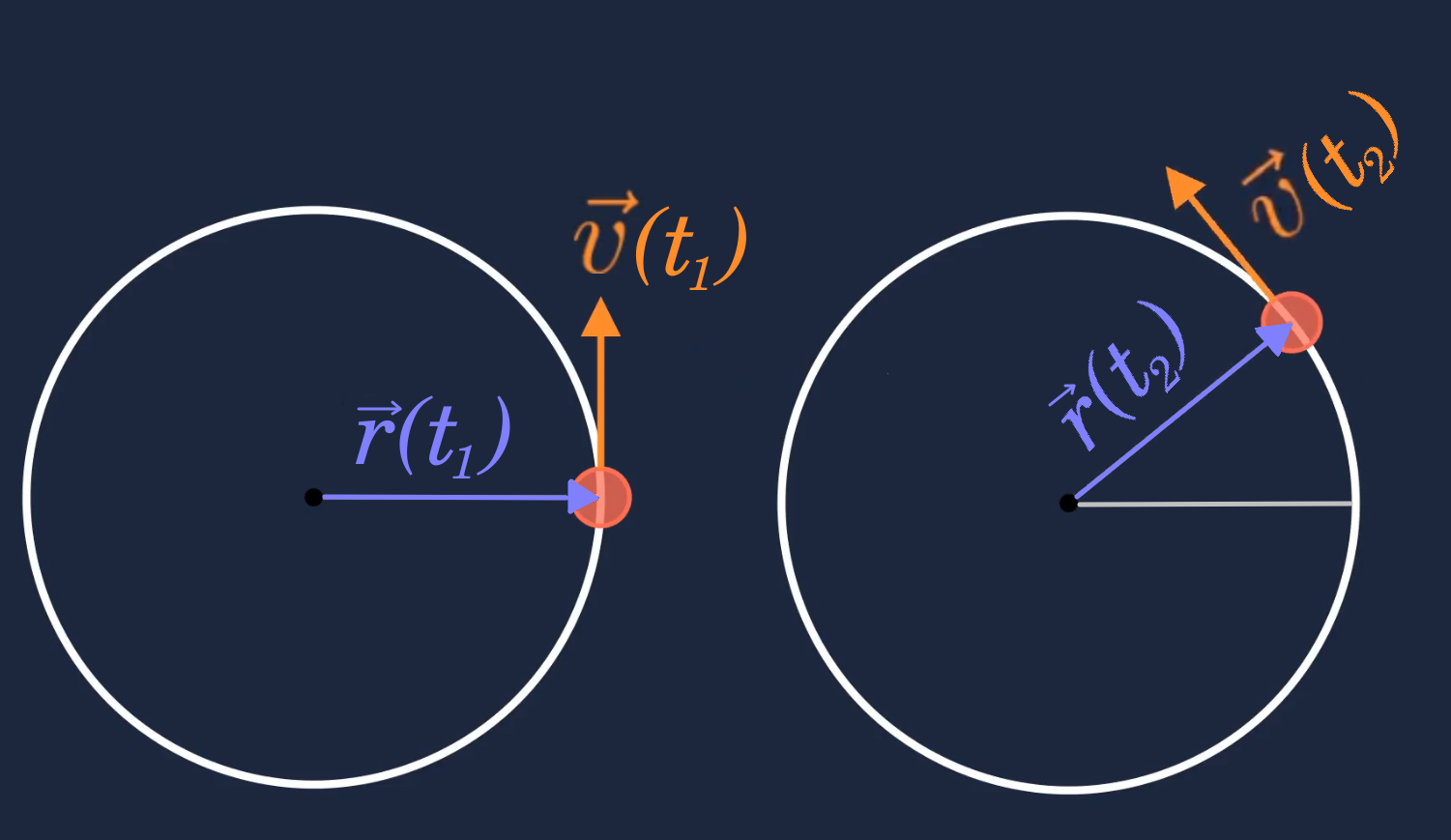
Der Geschwindigkeitsvektor kann über den folgenden Grenzwert definiert werden:
\(\begin{aligned} \vec{v}=\lim \limits_{\Delta t\to 0}\frac{\Delta \vec{r}}{\Delta t} \end{aligned}\)
wobei \(\Delta \vec{r}\) der Differenzvektor zwischen \(\vec{r}(t_1)\) und \(\vec{r}(t_2)\)
\(\begin{aligned} \Delta \vec{r}=\vec{r}(t_2)-\vec{r}(t_1) \end{aligned}\)
Kreisbewegung in Polarkoordinaten
Die Kreisbewegung lässt sich in Polarkoordinaten viel effizienter darstellen. Der Radiusvektor \(\vec{r}\) lautet in Polarkoordinaten:
\(\begin{aligned} \vec{r}=\begin{pmatrix} r\cdot cos(\varphi) \\ r\cdot sin(\varphi) \end{pmatrix} \end{aligned}\)
wobei \(\varphi\) der winkel zwischen dem Radiusvektor und der \(x\)-Achse ist.
Die Bahngeschwindigkeit kann nun über die zeitliche Ableitung vom Radiusvektor ermittelt werden:
\(\begin{aligned} \vec{v}&=\frac{d}{dt}\begin{pmatrix} r\cdot cos(\varphi) \\ r\cdot sin(\varphi) \end{pmatrix}\\& \\&=\begin{pmatrix} -r\cdot\frac{d\varphi}{dt}\cdot sin(\varphi) \\ r\cdot\frac{d\varphi}{dt}\cdot cos(\varphi) \end{pmatrix}\\ \\ &=\begin{pmatrix} -r\cdot\omega\cdot sin(\varphi) \\ r\cdot\omega\cdot cos(\varphi) \end{pmatrix} \end{aligned}\)
wobei \(\omega=\frac{d\varphi}{dt}\) die Winkelgeschwindigkeit ist.
