Differentialquotient berechnen
Ableitungsrechner
Mit dem Ableitungsrechner von Simplexy kannst du beliebige Funktionen Ableiten und den Differentialquotienten berechnen.
Differentialquotient
Der Differentialquotient wird verwendet um die Steigung einer Funktion an einem beliebigen Punkt zu berechnen.
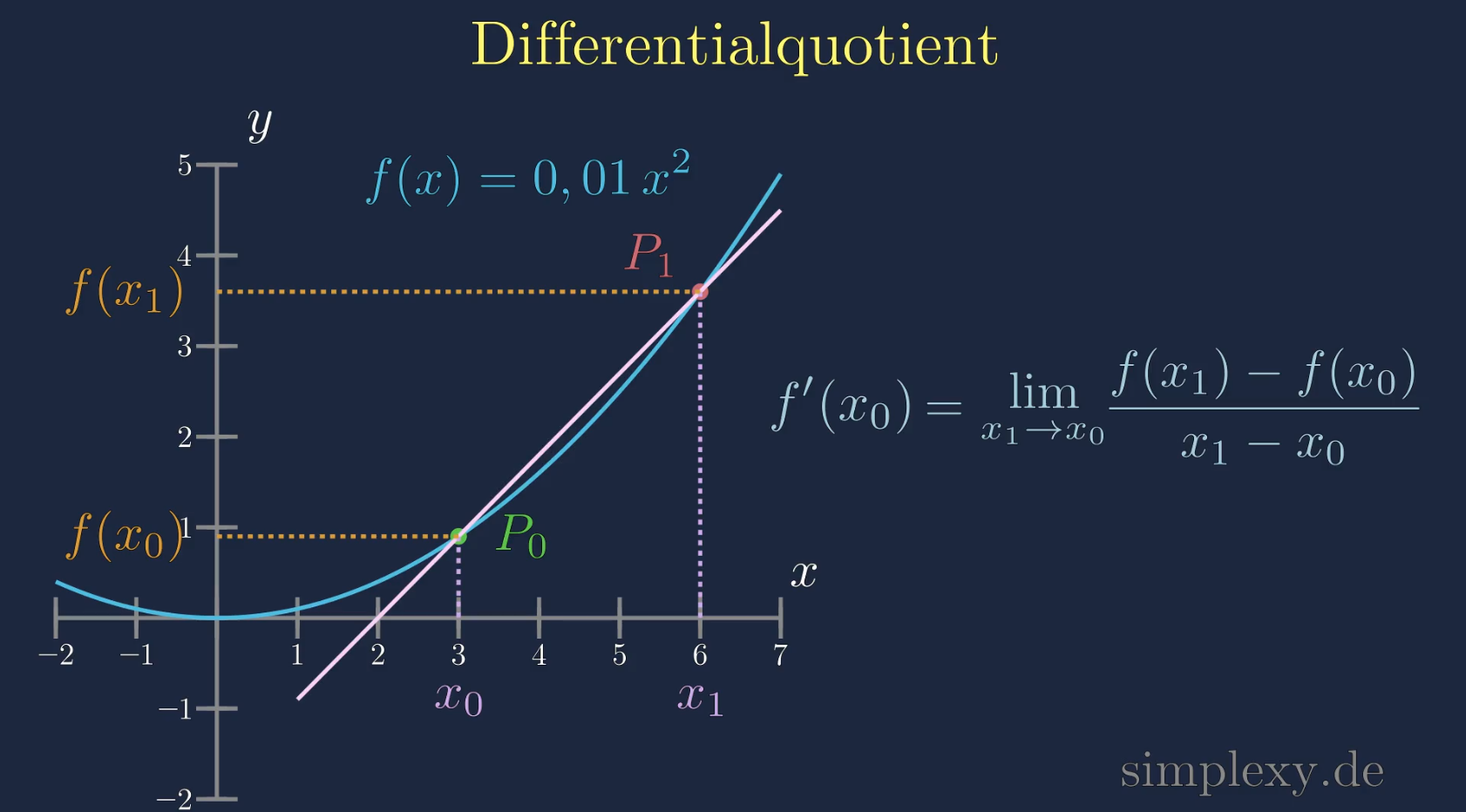
Differenzenquotient Formel
\(\begin{aligned} f'(x_0)=\lim\limits_{x _1\to x_0}\frac{f(x_1)-f(x_0)}{x_1-x_0} \end{aligned}\)
Dabei sind \(f(x_1)\) und \(x_1\) die Koordinaten des Punktes \(P_1\) und \(f(x_0)\) und \(x_0\) die Koordinaten des Punktes \(P_0\).
Steigung einer Funktion
Aus dem Thema Lineare Funktionen kennen wir bereits den Begriff Steigung einer Funktion.
Die Steigung einer Linearen Funktion berechnet sich über die Steigungsformel
\(\begin{aligned} m&=\frac{\Delta y}{\Delta x}\\ \\ &\text{bzw.}\\ \\ m&=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
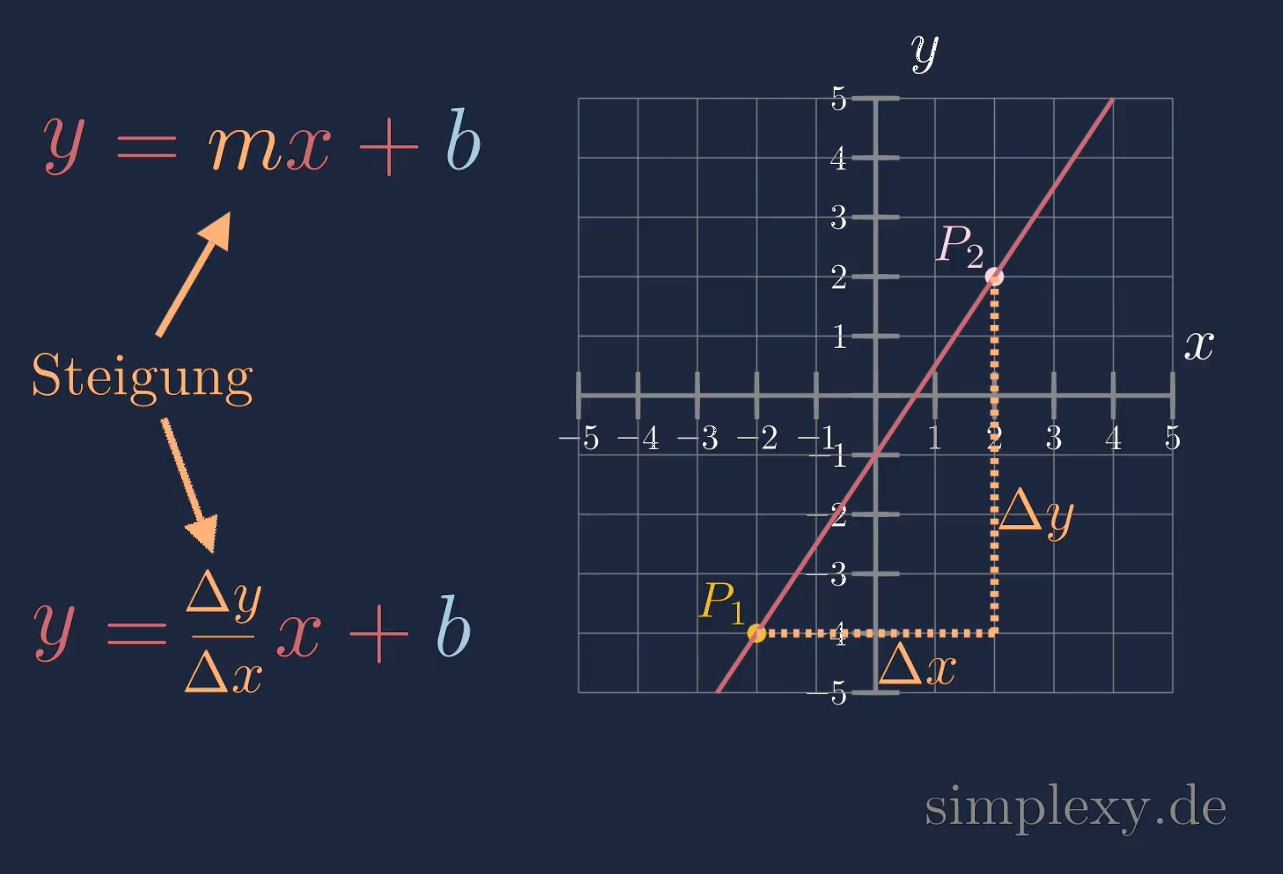
Mit der Steigungsformel kann man die Steigung einer linearen Funktion aus zwei beliebigen Punkten \(P_1\) und \(P_2\) berechnen.
Eine lineare Funktion hat in jedem Punkt die gleich Steigung. Die Steigung \(m\) einer linearen Funktion ist eine Konstante Zahl.
Wir haben uns auch schon mit den Quadratischen Funktionen beschäftigt. Der Graph einer quadratischen Funktion wird parabel genannt.
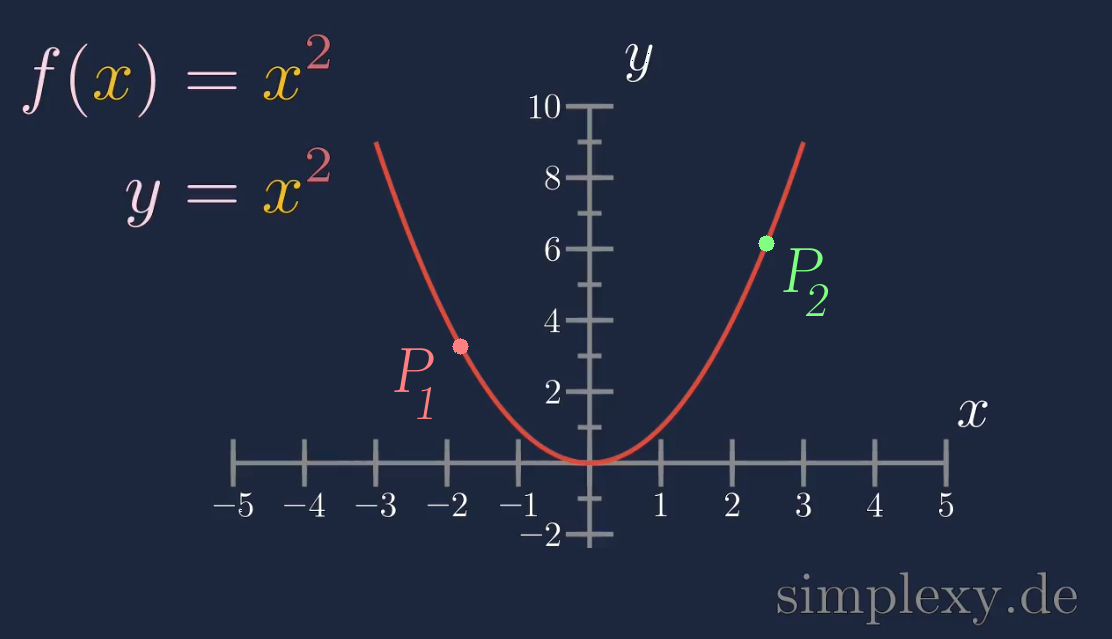
In dem letzten Beitrag zum Thema Differenzenquotient haben wir gesehen, wie man die mittlere Steigung einer Funktion zwischen zwei Punkten berechnen kann.

Um die mittlere Steigung der Funktion zwischen den zwei Punkten \(P_1\) und \(P_2\) zu berechnen, haben wir beide Punkte verbunden und so eine Sekante erhalten. Die Steigung \(m\) der Sekante entspricht der mittleren Steigung der Funktion zwischen den zwei Punkten
\(\begin{aligned} m&=\frac{f(x_2)-f(x_1)}{x_2-x_1}\\ \\ &=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
Differenzenquotient Formel
\(\begin{aligned} m=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
Dabei sind \(y_1\) und \(x_1\) die Koordinaten des ersten Punktes \(P_1\) und \(y_2\) und \(x_2\) die Koordinaten des zweiten Punktes \(P_2\).
Der Differenzenquotient gibt die mittlere Änderungsrate bzw. die durchschnittliche Steigung der Funktion im Bezug auf die zwei Punkte \(P_1\) und \(P_2\) an.
Nun stellt sich die Frage, wie man die Steigung einer Funktion an genau einem Punkt berechnen kann. Mit dem Differentialquotienten ist diese Berechnung möglich.
Differentialquotient Definition
Der Differentialquotient liefert einem die Steigung einer Funktion an einem beliebigen Punkt. Dazu benötigt man, wie in dem Video gezeigt, den Punkt \(P_0\) an dem die Steigung der Funktion berechnet werden soll. Zusätzlich benötigt man einen weiteren Punkt \(P_1\), dieser Punkt wird benötigt um eine Sekante zu bilden, welche beide Punkte mit einander verbindet.
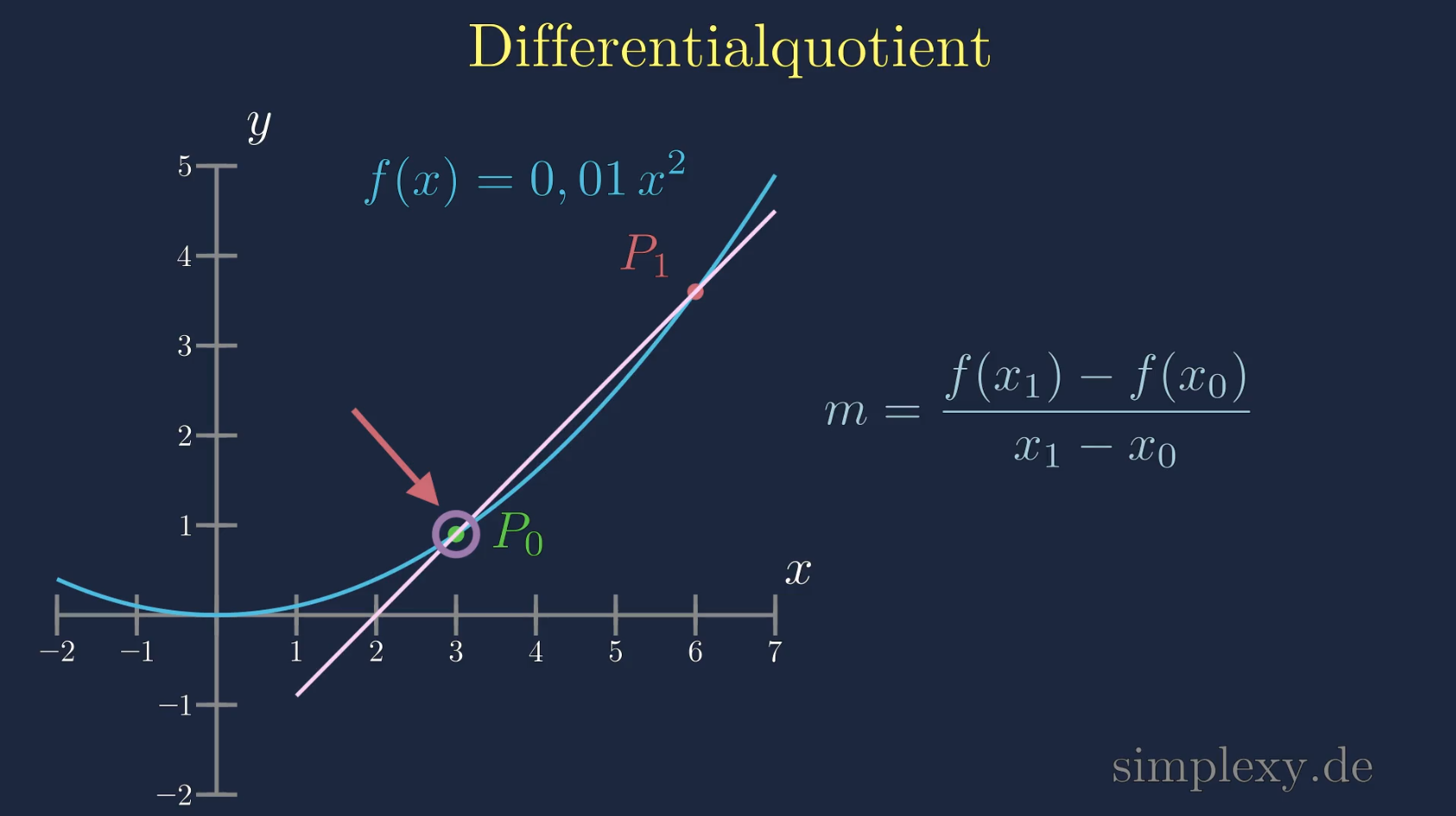
Die Steigung der Sekante zwischen den Punkten \(P_0\) und \(P_1\) berechnet sich über die Formel für den Differenzenquotient
\(\begin{aligned} m&=\frac{f(x_1)-f(x_0)}{x_1-x_0}\\ \end{aligned}\)
Um die Steigung der Funktion genau an dem Punkt \(P_0\) zu bekommen, kann man den Punkt \(P_1\) immer näher an den Punkt \(P_0\) schieben. Aus der Sekante wird so eine Tangente. Der einzige Punkt an dem die Tangente und die Funktion sich berühren ist der Punkt \(P_0\).
Die Steigung der Tangente entspricht der Steigung der Funktion an dem Punkt \(P_0\).
Der Vorgang, bei dem man den Punkt \(P_1\) zum Punkt \(P_0\) verschiebt, wird mathematisch als Grenzwert bezeichnet und über den limes \(\big(\,lim\,\big)\) ausgedrückt.
\(\begin{aligned} m=\lim\limits_{x _1\to x_0}\frac{f(x_1)-f(x_0)}{x_1-x_0} \end{aligned}\)
Statt \(m\) findet man oft für die Steigung der Tangente an dem Punkt \(P_0\) mit dem \(x\)-Wert \(x_0\) die Schreibweise \(f'(x_0)\)
\(\begin{aligned} f'(x_0)=\lim\limits_{x _1\to x_0}\frac{f(x_1)-f(x_0)}{x_1-x_0} \end{aligned}\)
Eine Tangente ist eine Gerade, die eine Funktion nur an einem einzigen Punkt berührt.
Je nachdem wo sich der Punkt \(P_0\) auf der Funktion befindet, erhält man eine andere Tangente mit einer anderen Steigung.
Die Steigung einer Kurve ist im Allgemeinen an jedem Punkt unterschiedlich.
Unterschied zwischen Differentialquotient und Differenzenquotient
Mit dem Differentialquotienten kann man die Steigung einer Funktion an einem Punkt berechnen. Die Formel dazu ähnelt der Formel für den Differenzenquotienten. Der Unterschied liegt in der Grenzwertbildung \(\lim\limits_{x _1\to x_0}\). Bei dem Differentialquotienten wird eine Tangete verwendet, deren Steigung gerade die Steigung der Funktion an dem Punkt entspricht. Beim Differenzenquotienten verbindet man die zwei betrachteten Punkte und brechnet die Steigung der Sekante.
\(\begin{aligned} \underbrace{f'(x_0)=\lim\limits_{x _1\to x_0}\underbrace{\frac{f(x_1)-f(x_0)}{x_1-x_0}}_{Differenzenquotient}}_{Differentialquotient} \end{aligned}\)
