Differenzenquotient berechnen
Ableitungsrechner
Mit dem Ableitungsrechner von Simplexy kannst du beliebige Funktionen Ableiten und den Differenzenquotienten berechnen.
Differenzenquotient
Der Differenzenquotient wird benötigt um die Steigung einer Funktion zwischen zwei Punkten zu berechnen.
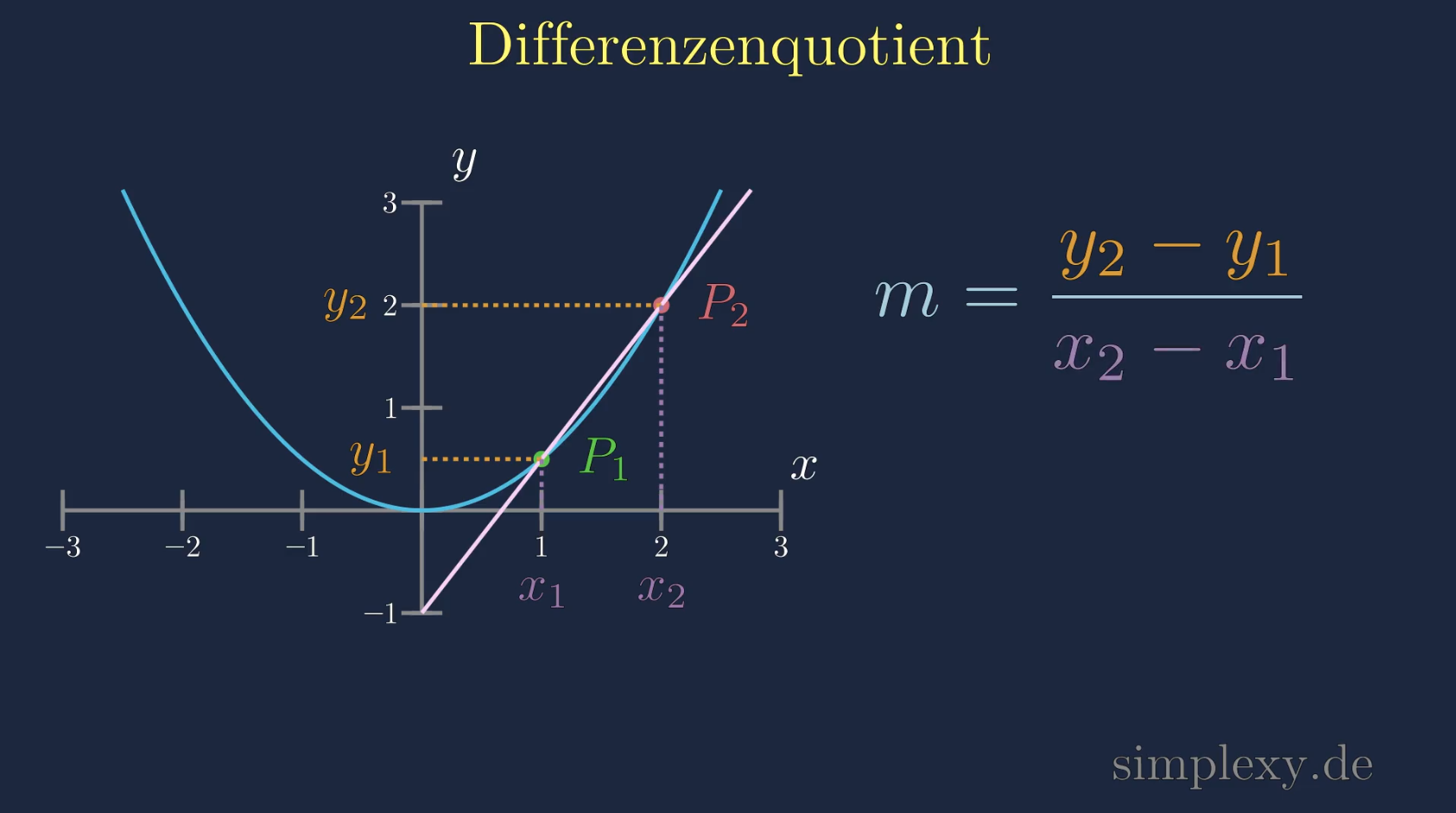
Differenzenquotient Formel
\(\begin{aligned} m=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
Dabei sind \(y_1\) und \(x_1\) die Koordinaten des ersten Punktes \(P_1\) und \(y_2\) und \(x_2\) die Koordinaten des zweiten Punktes \(P_2\).
Mittlere Steigung einer Funktion zwischen zwei Punkten
Aus dem Thema Lineare Funktionen kennen wir bereits den Begriff Steigung einer Funktion.
Die Steigung einer Linearen Funktion berechnet sich über die Steigungsformel
\(\begin{aligned} m&=\frac{\Delta y}{\Delta x}\\ \\ &\text{bzw.}\\ \\ m&=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
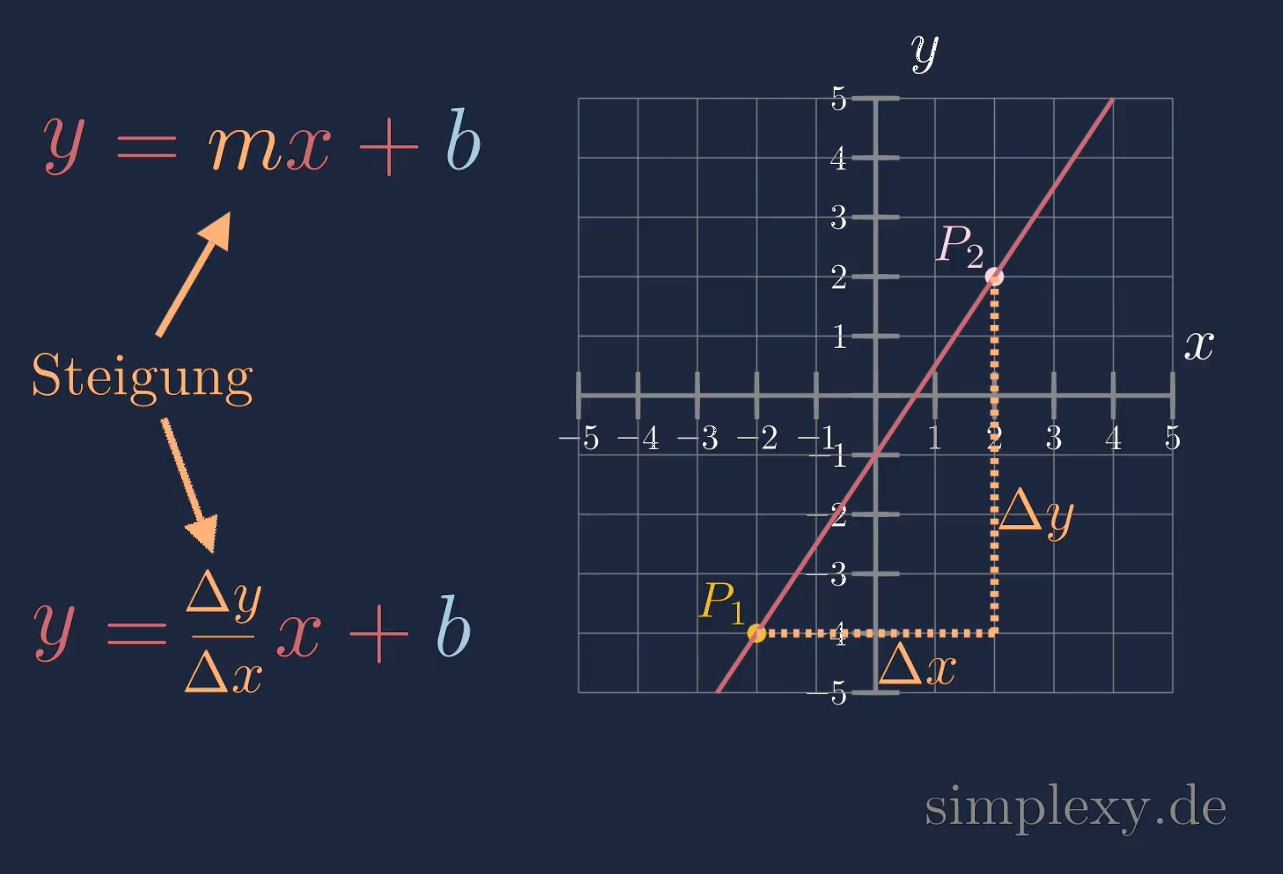
Mit der Steigungsformel kann man die Steigung einer linearen Funktion aus zwei beliebigen Punkten \(P_1\) und \(P_2\) berechnen.
Eine lineare Funktion hat in jedem Punkt die gleich Steigung. Die Steigung \(m\) einer linearen Funktion ist eine Konstante Zahl.
Wir haben uns auch schon mit den Quadratischen Funktionen beschäftigt. Der Graph einer quadratischen Funktion wird parabel genannt.
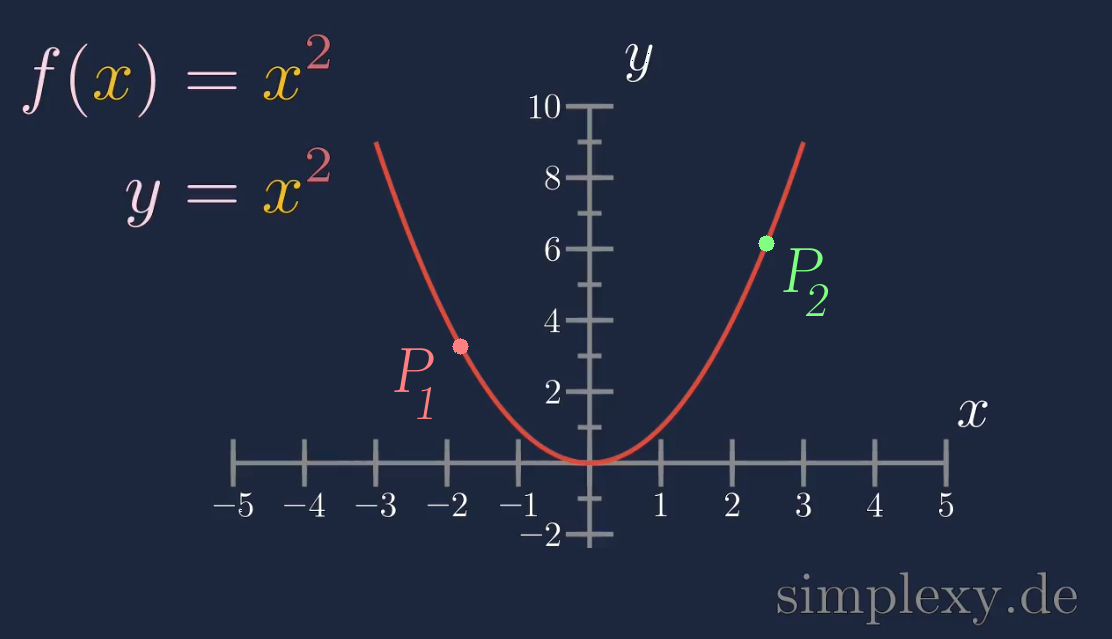
Nun muss man sich überlegen wie man bei einer Parabel oder jeder anderen Kurve die Steigung (Krümmung) definiert. Bei der oben abgebildeten Parabel ist es leicht zu sehen, dass die Steigung zwischen zwei beliebigen Punkten auf der Parabel unterschiedlich sein wird für verschiedene Punkte. Die Steigung wird also von der Wahl der zwei Punkte abhängen.
Bei Kurven ist die Steigung zwischen zwei Punkten, im Allgemeinen, nicht konstant. Die Steigung hängt von der Wahl der Punkte ab.
Differenzenquotient Definition
Der Differenzenqoutient zwischen zwei Punkten \(P_1\) und \(P_2\) auf einer Funktion \(f(x)\) berechnet sich über die Steigung der Sekenate welche entsteht, wenn die zwei Punkte über den direktesten Weg verbunden werden. Man geht bei der Berechnung der Steigung von der Sekante genau so vor, wie bei der Berechung von der Steigung einer Linearen Funktion.

Die Steigung der Sekante wird Differenzenquotient gennant und berechnet sich über die Formel:
\(\begin{aligned} m&=\frac{f(x_2)-f(x_1)}{x_2-x_1}\\ \\ &=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
Der Differenzenquotient gibt die mittlere Änderungsrate bzw. die durchschnittliche Steigung der Funktion im Bezug auf die zwei Punkte \(P_1\) und \(P_2\).
Je nach dem wo die Punkte auf einer Funktion liegen, erhält man im Allgemeinen eine andere Steigung der Sekante.
Hinweis
In der Mathematik schriebt man für die Differenz zweier Werte oft das Zeichen \(\Delta\) (griechischer Buchstebe "Delta"). Daher findet man für den Differenzenquotient manchmal die Schriebweise:
\(\begin{aligned} m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1} \end{aligned}\)
Der Differenzenquotient und die Steigung einer Geraden bzw. die Steigung einer linearen Funktion sind identisch. Es gibt lediglich einen Unterschied in der Schreibweise. Die Formel für den Differenzenquotienten und die Formel für die Steigung einer Geraden sind mathematisch gesehen gleich.
Mit dem Differenzenquotient erhält man nur die durchschnittliche Steigung einer Kurve zwischen zwei Punkten. Man bekommt damit nicht die "absolute" Steigung einer Kurve. Dazu benötigt man einen weiteren Schritt, der uns zum Differentialquotienten führt. Über den Differentialquotienten kann man die Steigung einer Kurve an einem beliebigen Punkt berechnen. Der Differentialquotient ist eine Grenzwertbildung des Differenzenquotienten. Nun wollen wir noch einige Beispiele berechnen.
Beispiele
Beispiel 1
Gegeben Sei die Funktion
\(\begin{aligned} f(x)=\frac{1}{2}x^2 \end{aligned}\)
und die Punkte
\(\begin{aligned} P_1&\text{ bei } x_1=1\\ P_2&\text{ bei } x_2=2\\ \end{aligned}\)
Berechne die mittlere Steigung der Funktion zwischen den zwei Punkten.
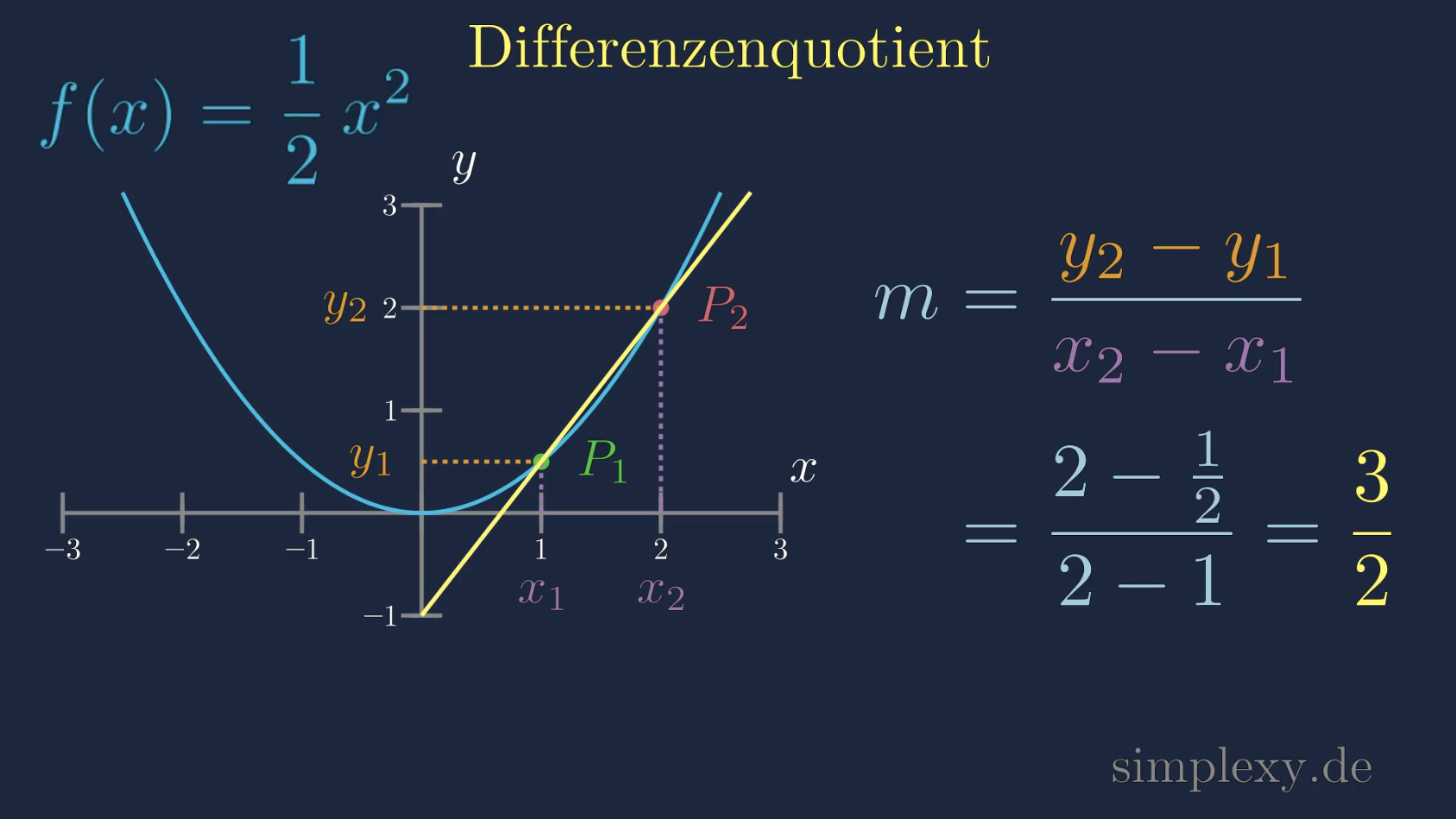
Lösung
Die Steigung der Funktion zwischen den zwei Punkten bekommen wir über den Differenzenquotienten. Für die Berechnung des Differenzenquotienten benötigen wir die \(x\) und \(y\) werte der zwei Punkte \(P_1\) und \(P_2\). Wir kennen ja den \(x\)-Wert des Punktes \(P_1\), dieser lautet \(x_1=1\). Wir kenne auch den \(x\)-Wert des \(P_2\) Punktes, dieser lautet \(x_2=2\). Nun müssen wir die \(y\)-Werte der zwei Punkte berechnen. Dazu setzen wir die \(x\)-Werte in die Funktionsgleichung:
\(\begin{aligned} y_1=f(x_1)=\frac{1}{2}1^2=\frac{1}{2} \end{aligned}\)
\(\begin{aligned} y_2=f(x_2)=\frac{1}{2}2^2=2 \end{aligned}\)
Wir können jetzt die Werte in die Formel des Differenzenquotienten einsetzten und damit die Steigung der Sekante berechnen, die gebildet wird wenn man die zwei Punkte \(P_1\) und \(P_2\) durch eine Gerade verbindet:
\(\begin{aligned} m&=\frac{y_2-y_1}{x_2-x_1}\\ \\ &=\frac{2-\frac{1}{2}}{2-1} \\ \\ &=\frac{\frac{3}{2}}{1}=\frac{3}{2} \end{aligned}\)
Die mittlere Steigung der Funktion \(f(x)\) zwischen den Punkten \(P_1\) und \(P_2\) betägt \(m=\) \(\frac{3}{2}\).
Beispiel 2
Bestimme die Steigung der Funktion
\(\begin{aligned} f(x)=x^2+x \end{aligned}\)
zwischen die Punkten \(x_1=3\) und \(x_2=11\). Nach der Formel für den Differenzenquotient berechnet man die mittlere Steigung über:
\(\begin{aligned} m&=\frac{f(x_2)-f(x_1)}{x_2-x_1}\\ \\ &=\frac{f(11)-f(3)}{11-3}\\ \\ &=\frac{11^2+11-(3^2+3)}{8}\\ \\ &=15 \end{aligned}\)
Über den Differenzenquotient haben wir die Steigung \(m=15\) für die Funktion \(f(x)\) zwischen den zwei Punkten berechnet.
