Gleichförmige Bewegung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Gleichförmige Bewegung
Du möchtest wissen was eine gleichförmige Bewegung ist? Dann schau dir am besten das untere Video an. Dort findest du eine leichte Erklärung der gleichförmigen Bewegung und einige Beispiele.
Gleichförmige Bewegung leicht erklärt
In der Physik versteht man unter einer gleichförmigen Bewegung eine geradlinige Bewegung, bei der die Geschwindigkeit konstant ist. Eine konstante Geschwindigkeit geht einher damit, dass die Beschleunigung gleich Null ist. Auf einen Körper der eine gleichförmigen Bewegung ausführt, wirken keine äußeren Kräfte, die Bewegung findet ohne einen Richtungswechsel statt.
Objekte die ohne Antrieb im Weltraum herum schweben, bewegen sich gleichförmig. Ihre Richtung und ihre Geschwindigkeit bleibt erhalten. Erst wenn ein Objekt in die Nähe eines Sterns oder eines Planten kommt, ändern sich die Geschwindigkeit und die Richtung. Dann führt das Objekt keine gleichförmige Bewegung mehr aus.
Merkmale einer gleichförmigen Bewegung
-
Bewegung entlang einer geraden linie
-
ohne Richtungswechsel
-
konstante Geschwindigkeit
-
keine Beschleunigung
Gleichförmige Bewegung Formeln
Eine Bewegung in der Physik wird mit der Strecke \(s\) der Geschwindigkeit \(v\) und der Zeit \(t\) beschrieben. Die Formel der gleichförmigen Bewegung stellt eine Beziehung zwischen diesen größen her.
Gleichförmige Bewegung Formel
\(\begin{aligned} v=\frac{s}{t} \end{aligned}\)
Dabei ist:
-
\(v\) die Geschwindigkeit in \([\frac{m}{s}]\)
-
\(s\) die zurückgelegte Strecke in \([m]\)
-
\(t\) die Zeit in \([s]\)
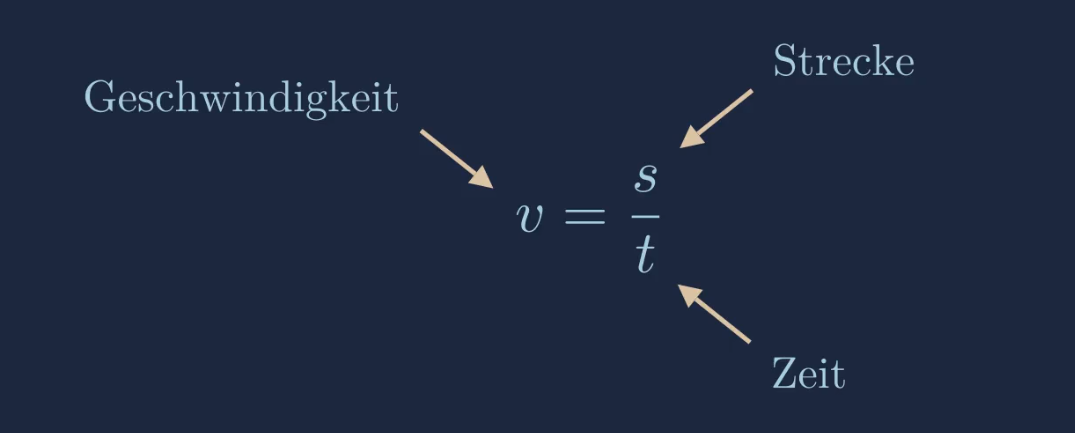
Diese Formel kennt man bereits aus der Geschwindigkeit. Wie bereits erwähnt ist die Geschwindigkeit bei der gleichförmigen Bewegung konstant. Über diese Formel kann man auch die zurückgelegte Strecke \(s\) berechnen. Dazu muss man die Formel nach \(s\) umstellen.
\(\begin{aligned} s=v\cdot t \end{aligned}\)
Die zurückgelegte Strecke ist das Produkt aus der Geschwindigkeit und der Zeit. Manchmal findet man die Formel auch mit einem \(s_0\)
\(\begin{aligned} s=v\cdot t+s_0 \end{aligned}\)
Dabei ist \(s_0\) die Anfangsstrecke. Die Anfangsstrecke benötigt man dann, wenn man eine Messung durchführt und die Bewegung nicht bei der Strecke Null startet. In der Regel ist die Anfangsstrecke jedoch Null (\(s_0=0\)) und wird daher weggelassen.
Zuletzt kann man die Formel der gleichförmigen Bewegung nach der Zeit \(t\) umstellen.
\(\begin{aligned} t=\frac{s}{v} \end{aligned}\)
Diese Formel ist relevant, wenn man beispielsweise berechnen möchte wie lange es dauert bis ein Körper ein bestimmtes Ziel erreicht bzw. eine bestimmte Strecke zurückgelegt hat.
Einheiten
Die Geschwindigkeit wird in Meter pro Sekunde \([\frac{m}{s}]\) angegeben. Die Strecke wird in Meter \([m]\) angegeben. Die Zeit wird in Sekunden\([s]\) angegeben.
Gleichförmige Bewegung Beispiel
Um die Anwendung der Formeln zu verdeutlichen werden wir nun zwei Beispiele berechnen:
Beispiel 1
Ein Auto ist mit einer Geschwindigkeit von \(50\frac{km}{h}\) unterwegs. Die Geschwindigkeit des Autos ist konstant und das Auto bewegt sich entlang einer geraden Linie. Das Auto ist \(4\) Stunden unterwegs. Welche Strecke hat das Auto in dieser Zeit zurück gelegt.
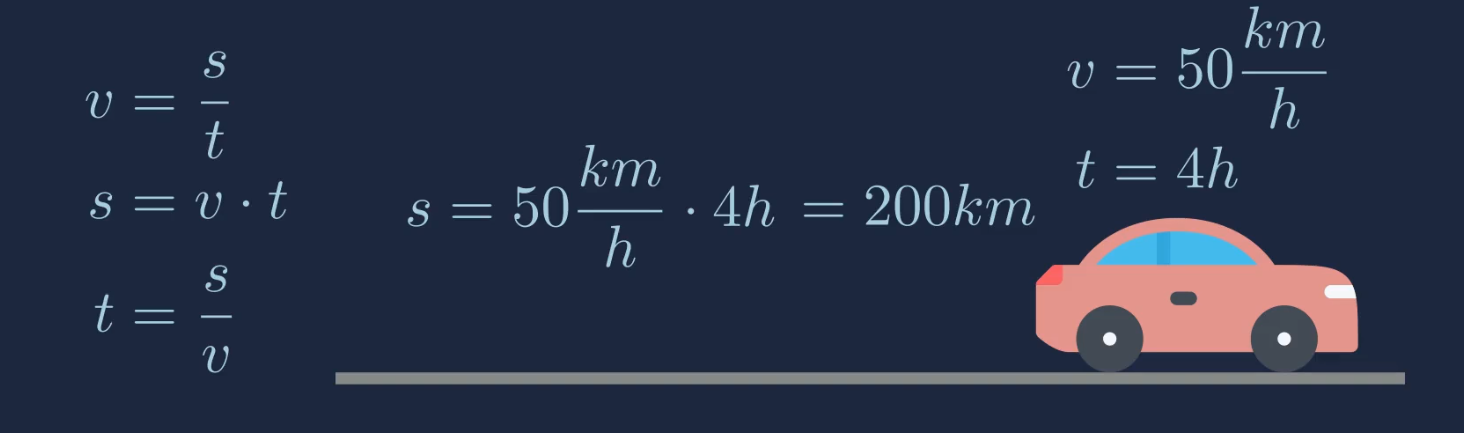
Um die zurückgelegte Strecke \(s\) zu berechnen, müssen wir die Formel
\(\begin{aligned} s=v\cdot t \end{aligned}\)
verwenden. Dazu müssen wir die gegebenen Werte für die Geschwindigkeit \(v=50\frac{km}{h}\) und der Fahrzeit \(t=4h\) in die Formel einsetzen.
\(\begin{aligned} s=50\frac{km}{h}\cdot 4h=200km \end{aligned}\)
Das Auto hat eine Strecke von \(s=200km\) zurückgelegt.
Beispiel 2
Mit einem Revolver wird auf eine Flasche geschossen, die sich \(14\) Meter entfernt befindet. Die Kugel trifft die Flasche in genau \(0,\!02s\). Dabei wird angenommen, dass sich die Kugel gleichförmig bewegt hat. Wie schnell war die Kugel?

Um die Geschwindigkeit der Kugel zu berechnen, müssen wir folgende Formel verwenden:
\(\begin{aligned} v=\frac{s}{t} \end{aligned}\)
Nun müssen wir die gegeben Werte in die Formel einsetzten. Wir erhalten:
\(\begin{aligned} v=\frac{14m}{0,\!02}=700\frac{m}{s} \end{aligned}\)
Die Kugel ist mit einer Geschwindigkeit von \(v=700\) Meter pro Sekunden geflogen.
Gleichförmige Bewegung Diagramme
Die Beziehungen zwischen der Strecke, der Geschwindigkeit und der Zeit bei der gleichförmigen Bewegung können in Diagrammen dargestellt werden. Dazu gibt es das Weg-Zeit-Diagramm, das Geschwindigkeit-Zeit-Diagramm und das Beschleunigungs-Zeit-Diagramm.
Weg-Zeit-Diagramm
Beim Weg-Zeit-Diagramm der gleichförmigen Bewegung wird auf der x-Achse die Zeit \(t\) aufgetragen und auf der y-Achse die Strecke \(s\).
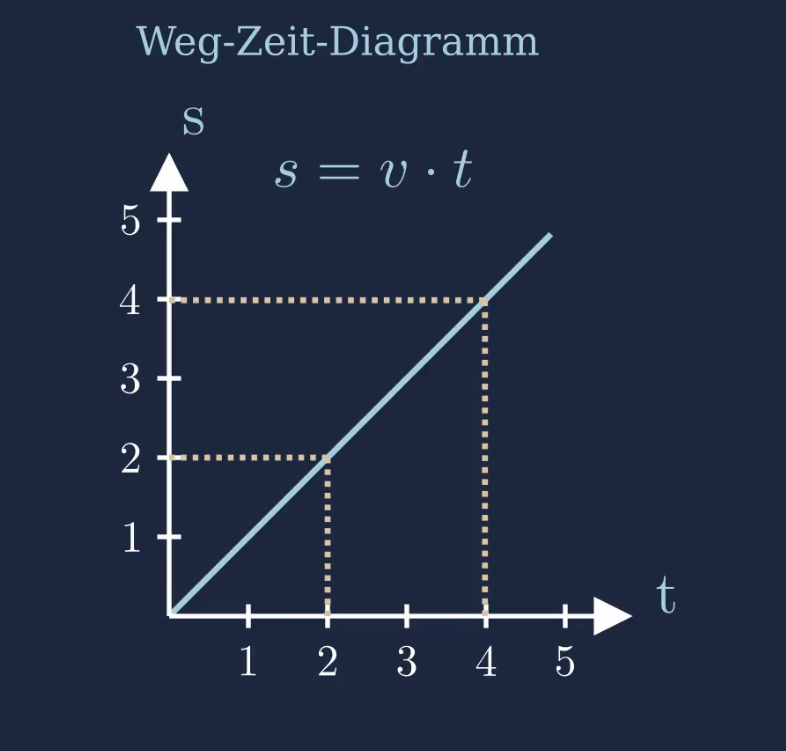
Die zurückgelegte Strecke nimmt im laufe der Zeit linear zu. Dies folgt daraus, dass die Geschwindigkeit konstant ist. Der lineare Zusammenhang zwischen der Strecke und der Zeit wird mathematisch als Weg-Zeit-Gesetz beschrieben.
Weg-Zeit-Gesetz
\(\begin{aligned} s(t)=v\cdot t \end{aligned}\)
Die zurückgelegte Strecke \(s\) ist eine lineare Funktion, die von der Zeit \(t\) abhängt. Die Geschwindigkeit \(v\) ist konstant und entspricht der Steigung der linearen Funktion.
Die Steigung des Funktionsgraphen der Strecke \(s\) entspricht der Geschwindigkeit \(v\).
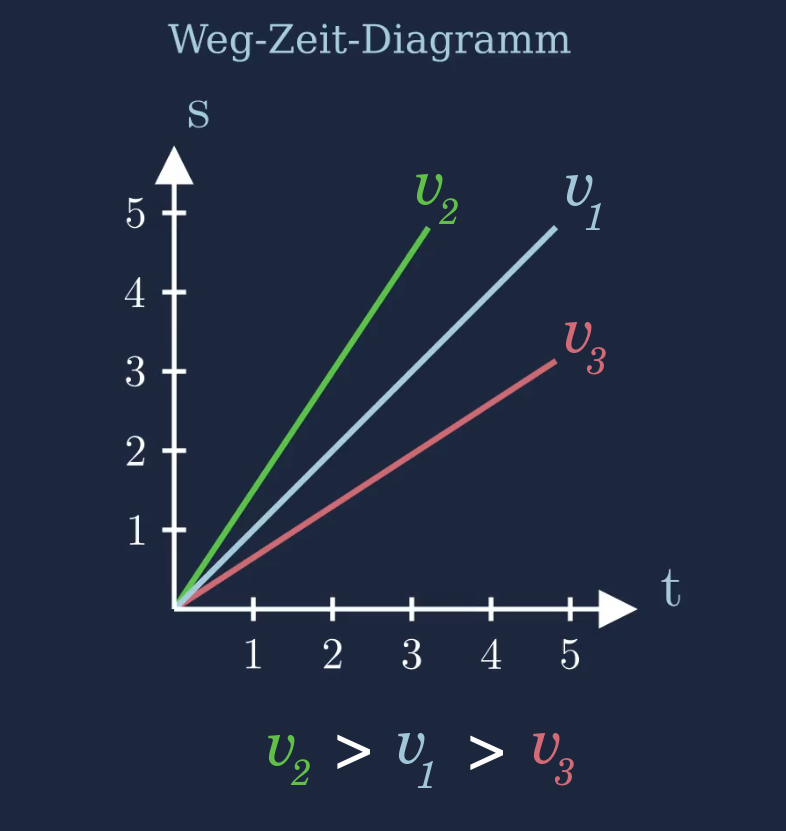
Je größer die Geschwindigkeit ist, desto größer ist die Steigung. Je kleiner die Geschwindigkeit ist, desto kleiner ist die Steigung.
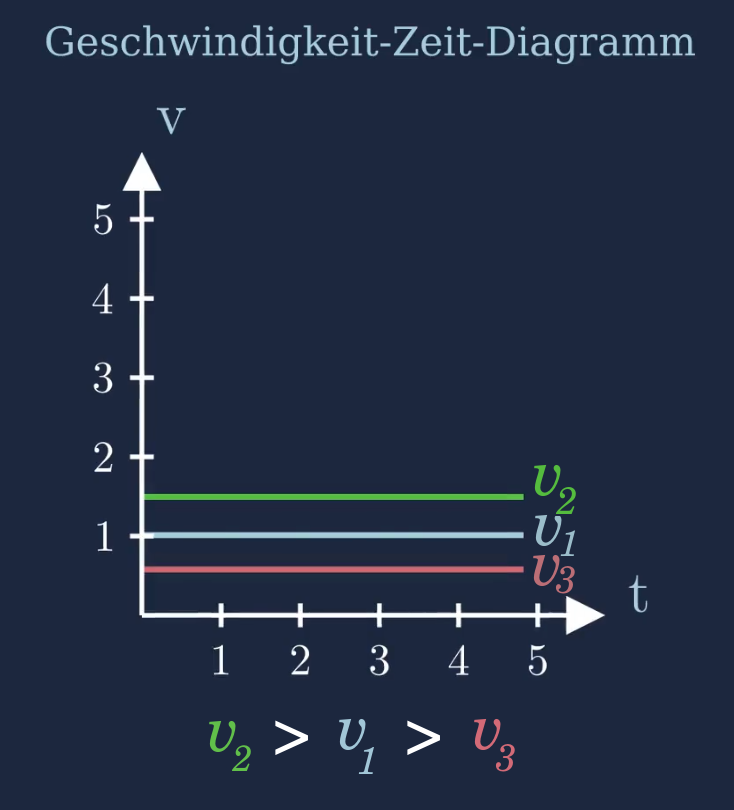
Geschwindigkeit-Zeit-Diagramm
Beim Geschwindigkeit-Zeit-Diagramm wird auf der x-Achse die Zeit aufgetragen und auf der y-Achse die Geschwindigkeit. Da die Geschwindigkeit bei der gleichförmigen Bewegung permanent konstant ist, sieht man im Diagramm nur eine horizontale Linie (konstante Funktion).
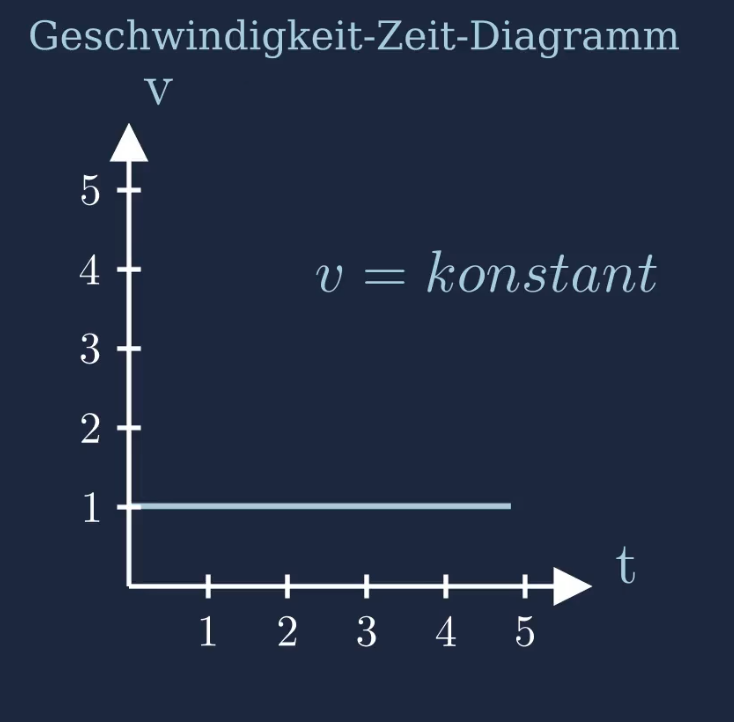
Das Geschwindigkeits-Zeit-Gesetz gibt vor, dass die Geschwindigkeit konstant ist. Dies haben wir bereits als Bedingung für die gleichförmige Bewegung definiert.
Geschwindigkeits-Zeit-Gesetz
Bei der gleichförmigen Bewegung ist die Geschwindigkeit stets konstant.
Je größer die Geschwindigkeit ist, desto "höher" liegt die horizontale Linie. Je kleiner die Geschwindigkeit ist, desto "niedriger" liegt die horizontale Linie.