Gleichmäßig beschleunigte Bewegung
Online Rechner mit Rechenweg
Der Online Rechner von Simplexy kann dir beim berechnen vieler Aufgaben helfen. Probiere den Rechner mit Rechenweg aus.
Gleichmäßig Beschleunigte Bewegung
Du möchtest wissen was die gleichmäßig beschleunigte Bewegung ist? Dann schau dir am besten das untere Video an. Dort wirst du auch lernen wie man mit dem Weg-Zeit-Diagramm, Geschwindigkeit-Zeit-Diagramm und dem Beschleunigung-Zeit-Diagramm die beschleunigte Bewegung beschreiben kann.
Gleichmäßig beschleunigte Bewegung erklärt
Bei der gleichmäßig beschleunigten Bewegung wird ein körper mit konstanter Beschleunigung bewegt. Ein Beispiel dafür ist der Freie Fall, bei dem die Erdbescheunigung konstant mit \(g=9,\!81\frac{m}{s^2}\) wirkt. Lässt du einen Ball aus einem hohen Haus fallen, so wird der Ball bis zum Aufprall immer schneller. Dies liegt an der Erdbescheunigung, welche die Fallgeschwindigkeit allmählich erhöht. Du möchtest wiederholen was die Beschleunigung ist, dann werf einen Blick auf dieses Video.
Beschleunigung
Die Beschleunigung \(a\) gibt an, wie sich die Geschwindigkeit ändert.
Die Beschleunigung hat die Einheit \([\frac{m}{s^2}]\).
Bewegt sich eine Körper mit einer Beschleunigung von \(10\frac{m}{s^2}\), so ändert sich dessen Geschwindigkeit um \(10\frac{m}{s}\) innerhalb jeder Sekunde.
Die gleichmäßig beschleunigte Bewegung ist eine Bewegung deren Richtung und Beschleunigung konstant sind.
Gleichmäßig beschleunigte Bewegung Formeln
Zur Beschreibung der gleichmäßig beschleunigten Bewegung werden drei Gesetze herangezogen.
Gesetze der gleichmäßig beschleunigten Bewegung
-
Beschleunigung-Zeit-Gesetz
-
Geschwindigkeit-Zeit-Gesetz
-
Weg-Zeit-Gesetz
Beschleunigung-Zeit-Gesetz
Mit dem Beschleunigung-Zeit-Gesetz wird die Beschleunigung im Verlauf der Zeit beschrieben. Bei der gleichmäßig beschleunigten Bewegung ist die Beschleunigung jedoch zeitlich konstant. Sie verändert sich somit nicht.
Beschleunigung-Zeit-Gesetz
\(\begin{aligned} a=\text{konstant} \end{aligned}\)
Im Beschleunigung-Zeit-Diagramm kann dies verdeutlicht werden.
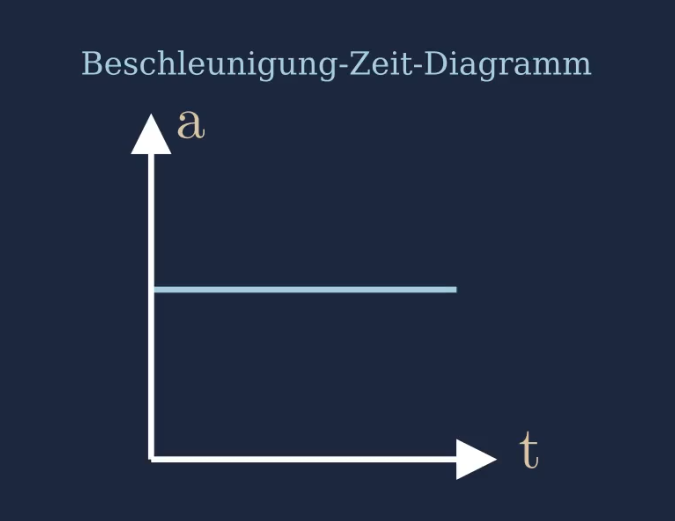
Die Beschleunigung wird durch eine konstante Funktion dargestellt, deren Wert zu jeder Zeit gleich bleibt.
Geschwindigkeit-Zeit-Gesetz
Das Geschwindigkeit-Zeit-Gesetz beschreibt das zeitliche Verhalten der Geschwindigkeit. Aufgrund der konstanten Beschleunigung nimmt die Geschwindigkeit linear mit der Zeit zu.
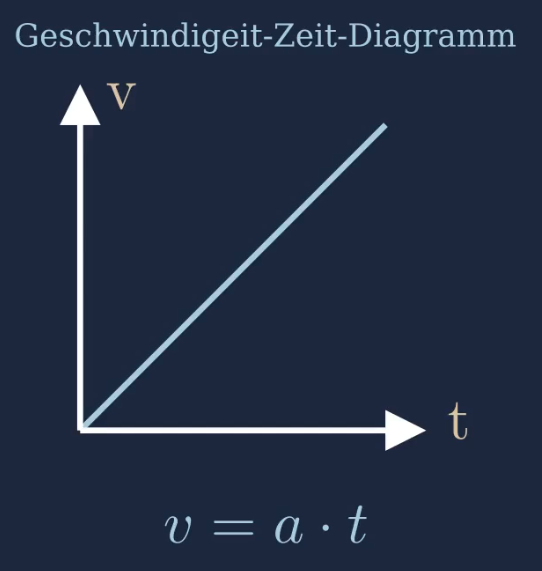
Bei einer Beschleunigung \(a=10\frac{m}{s^2}\) nimmt die Geschwindigkeit pro Sekunde um \(10\frac{m}{s}\) zu. Dieses Verhalten wird durch das Geschwindigkeit-Zeit-Gesetz beschrieben.
Geschwindigkeit-Zeit-Gesetz
\(\begin{aligned} v=a\cdot t+v_0 \end{aligned}\)
Dabei ist \(v_0\) die Anfangsgeschwindigkeit welche in der Regel Null ist.
Weg-Zeit-Gesetz
Das Weg-Zeit-Gesetz beschreibt den zurückgelegten Weg im laufe der Zeit. Da bei der beschleunigten Bewegung die Geschwindigkeit linear zunimmt, kann eine immer größere Teilstrecke in einer bestimmten Zeit zurückgelegt werden. Die zurückgelegt Strecke \(s\) nimmt quadratisch mit der Zeit zu. Dieses Verhalten wird im Weg-Zeit-Diagramm dargestellt.
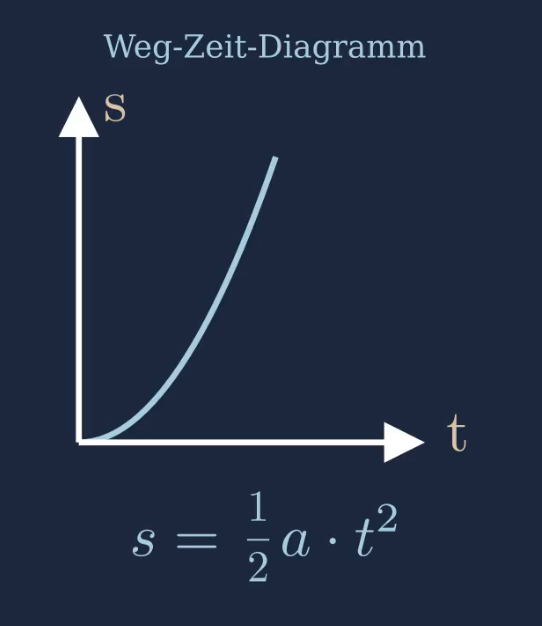
Da sich die Geschwindigkeit im laufe der Zeit lineare erhöht, nimmt die zurückgelegt Strecke quadratisch mit der Zeit zu. Dies wird vom Weg-Zeit-Gesetz beschrieben.
Weg-Zeit-Gesetz
\(\begin{aligned} s=\frac{1}{2}a\cdot t^2+s_0 \end{aligned}\)
Wobei \(s_0\) die Anfangsstrecke ist, welche in der Regel Null ist.
Gleichmäßig beschleunigte Bewegung Diagramme
Die gleichmäßig beschleunigte Bewegung kann mittels drei Diagramme dargestellt werden. Diese haben wir bereits im oberen Abschnitt behandelt. Der Vollständigkeit halber sieht man im unteren Bild alle drei Diagramme neben einander:
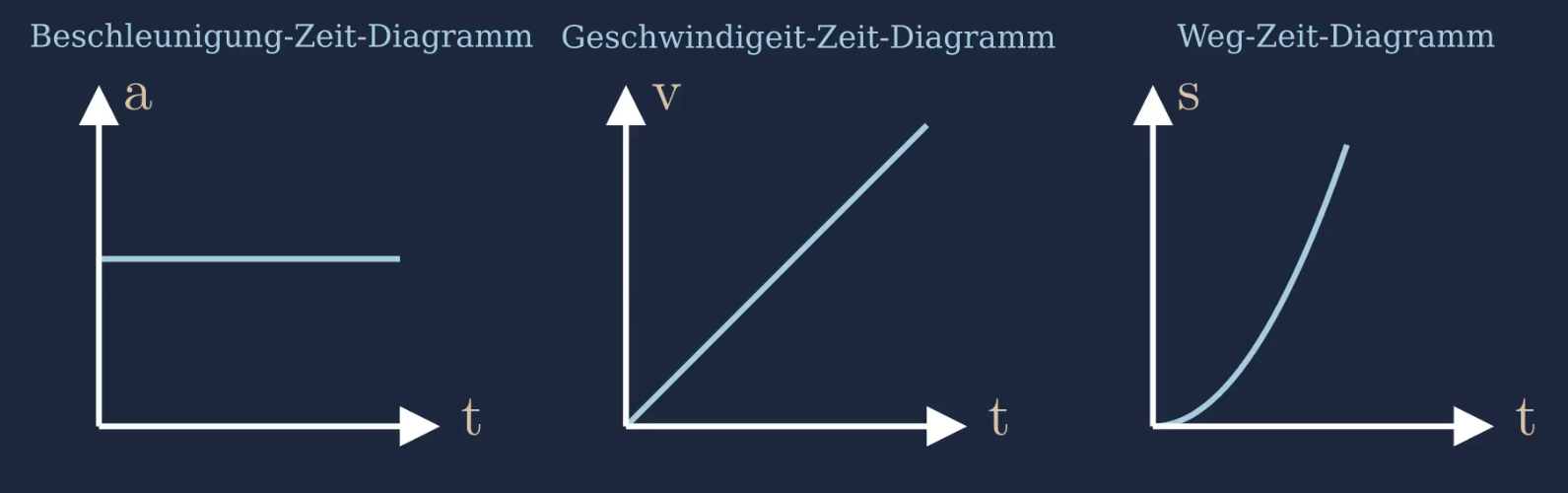
Wie verändern sich die Diagramme der gleichmäßig beschleunigten Bewegung, wenn eine größere oder eine kleinere Beschleunigung betrachtet wird.
Je größer die Beschleunigung ist, desto höher liegt die horizontale Linie der Beschleunigung im Beschleunigung-Zeit-Diagramm. Damit nimmt die Geschwindigkeit schneller zu und der Graph im Geschwindigkeit-Zeit-Diagramm hat eine größere Steigung. Dies hat wiederum Einfluss auf die zurückgelegte Strecke. Der Graph der zurückgelegten Strecke wird gestreckt.
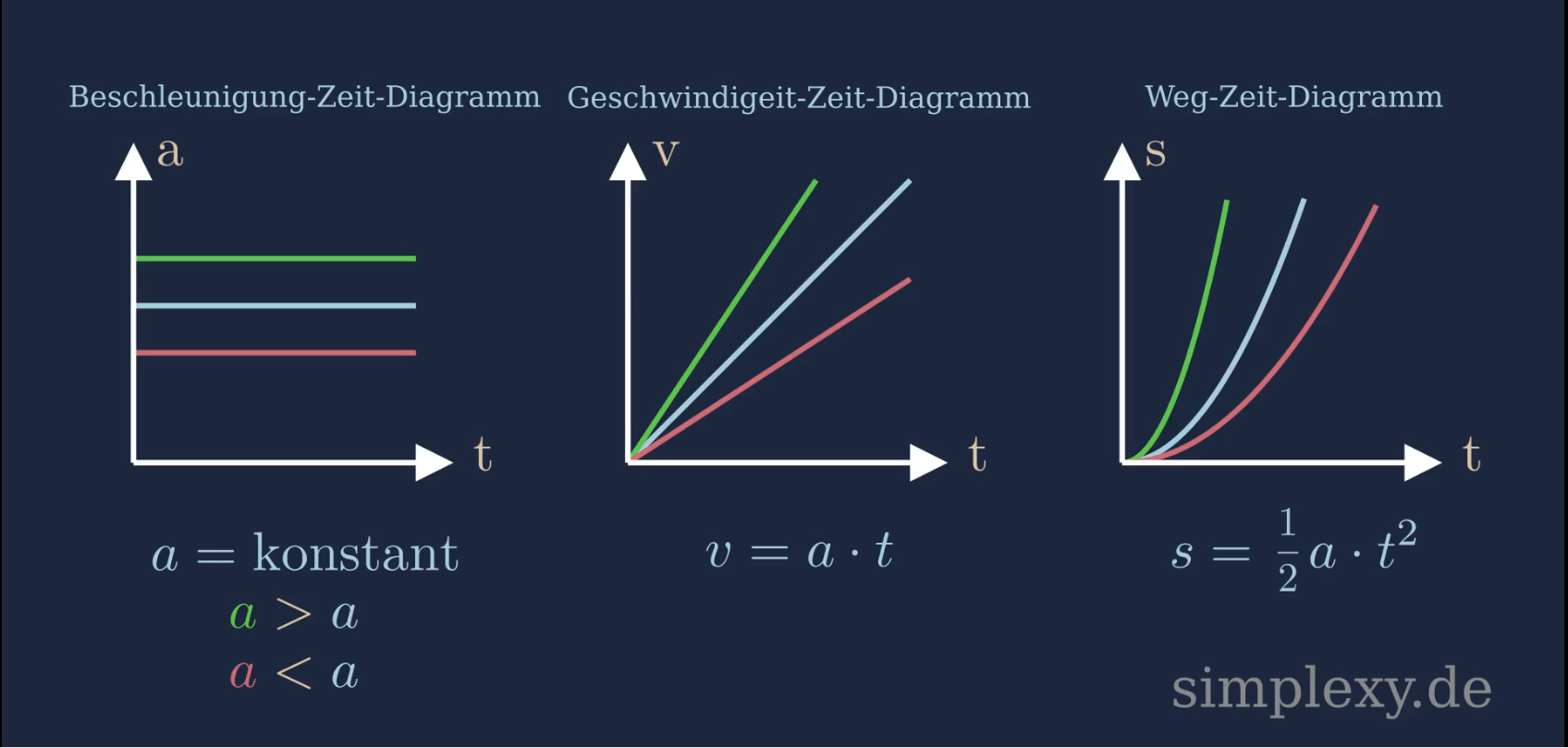
Je kleiner die Beschleunigung ist, desto niedriger liegt der horizontale Linie der Beschleunigung im Beschleunigung-Zeit-Diagramm. Die Geschwindigkeit nimmt nicht mehr so schnell zu. Der Graph der Geschwindigkeit besitzt eine kleinere Steigung und wird somit flacher. Dies hat ebenfalls Einfluss auf die zurückgelegte Strecke. Der Graph der zurückgelegten Strecke wird gestaucht.
Beispiel gleichmäßig beschleunigte Bewegung
Es folgt nun ein Beispiel der gleichmäßig beschleunigten Bewegung. Dabei werden wir den Freien Fall betrachten, bei dem die Erdbescheunigung konstant mit etwa \(a=10\frac{m}{s^2}\) wirkt.
Freier Fall
In diesem Beispiel betrachten wir einen Ball, der aus einer Höhe fallen gelassen wird. Die einzige auf den Ball wirkende Kraft ist die Erdanziehung. Es wirkt also nur die Erdbeschleunigung mit \(a=10\frac{m}{s^2}\).
Welche Geschwindigkeit hat der Ball nach 2 Sekunden erreicht?
Um die Geschwindigkeit vom Ball berechnen zu können, verwenden wir das Geschwindigkeit-Zeit-Gesetz.
\(\begin{aligned} v(t)=a\cdot t+v_0 \end{aligned}\)
Da der Ball aus der Ruhe fallengelassen wird, ist die Anfangsgeschwindigkeit \(v_0=0\). In das Geschwindigkeit-Zeit-Gesetz setzen wir nun \(t=2s\) und \(a=10\frac{m}{s^2}\) ein, um die Geschwindigkeit des Balls nach \(2s\) zu berechnen:
\(\begin{aligned} v(t=2s)&=10\frac{m}{s^2}\cdot 2s\\ \\ &=20\frac{m}{s} \end{aligned}\)
Nach \(2s\) hat der Ball eine Geschwindigkeit von \(20\frac{m}{s}\) erreicht. Aus dem dazugehörigen Geschwindigkeit-Zeit-Diagramm kann man die lineare Zunahme der Geschwindigkeit des Balls ebenfalls entnehmen:
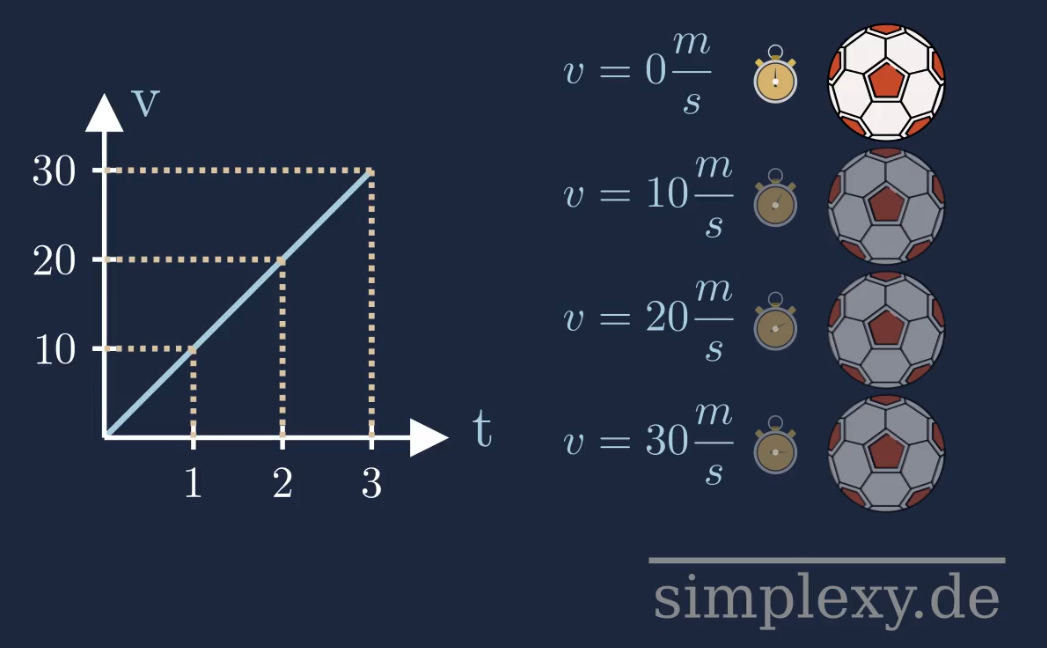
Welche Strecke hat der Ball nach 2 Sekunden zurückgelegt?
Um die zurückgelegte Strecke des Balls nach 2 Sekunden zu berechnen, müssen wir das Weg-Zeit-Gesetz verwenden.
\(\begin{aligned} s(t)=\frac{1}{2}a\cdot t^2+s_0 \end{aligned}\)
Dabei ist die Anfangsstrecke \(s_0=0\). Die zurückgelegte Strecke beginnt also dort wo der Ball fallengelassen wird. Nun setzen wir die Beschleunigung \(a=10\frac{m}{s^2}\) und die Zeit \(t=2s\) in das Weg-Zeit-Gesetz ein und erhalten:
\(\begin{aligned} s(t=2s)&=\frac{1}{2}\cdot 10\frac{m}{s^2}\cdot (2s)^2\\ \\&=20m \end{aligned}\)
Nach zwei Sekunden hat der Ball eine Strecke von \(20\) Metern zurückgelegt. Dies kann ebenfalls aus dem Weg-Zeit-Diagramm entnommen werden:
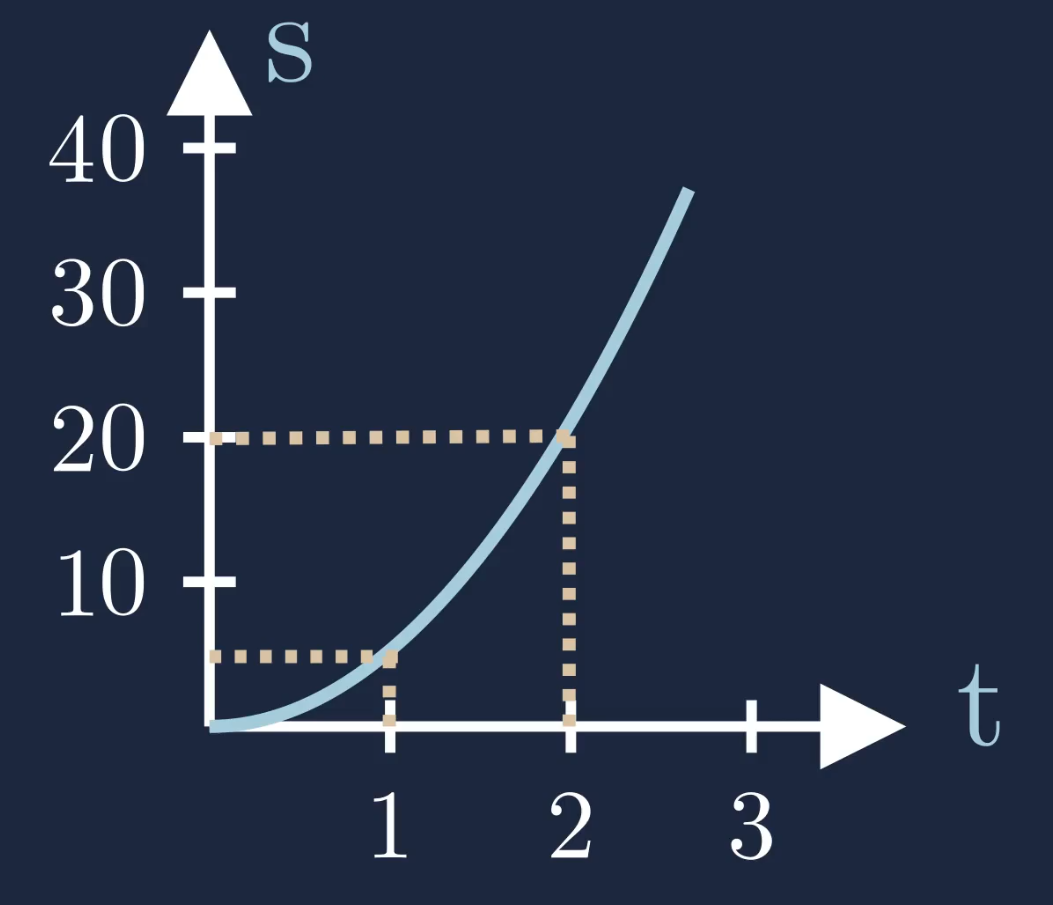
Du möchtest mehr über den Freien Fall wissen, dann werf einen Blick auf diesen Beitrag.
