Integralrechnung Überblick
Integralrechner
Du möchtest deine Lösungen Prüfen? Dann kannst du den Integralrechner von Simplexy nutzen. Mit dem Integralrechner kannst du sowohl die Stammfunktion berechnen als auch die Fläche unter einer Funktion berechnen. Probiere den Integralrechner jetzt aus...
Integralrechnung Überblick
In diesem Beitrag wirst du einen Überblick über das Thema Integralrechnung bekommen. Es werden viele Beispiel zum Thema Integralrechnung und Stammfunktion gerechnet.
Nachdem man in der Schule das Thema Ableitung behandelt hat, geht es meistens mit dem Thema Integralrechnung weiter. Sowohl die Differentialrechnung als auch die Integralrechnung sind wichtige Zweige der Analysis.
Die Analysis ist eine wichtige Disziplin in der Mathematik.
Die Integralrechnung wird oft verwendet um Flächen und Volumen zu berechnen. Mehr dazu werden wir weiter unten behandeln. Je nachdem ob man eine Fläche unter einer Funktion berechnen möchte oder lediglich die Stammfunktion einer Ausgangsfunktion, unterscheidet man zwischen einem bestimmten Integral und einem unbestimmten Integral. Beide Integrationsarten werden in diesem Beitrag behandelt. Wir fangen jedoch zunächst mit den Grundlagen der Integralrechnung an
Integralrechnung Grundlagen
Zwischen dem Integral einer Funktion und dem Ableiten einer Funktion gibt es einen Zusammenhang. Man nennt das Integrieren auch Aufleiten.
Das Integrieren ist die Umkehrung der Ableitung
\(\underbrace{F(x)}_{\text{Stammfunktion}}\overbrace{\longleftarrow}^{\text{integrieren}} f(x)\overbrace{\longrightarrow}^{\text{ableiten}} \underbrace{f'(x)}_{\text{1.Ableitung}}\)
\(\underbrace{F(x)}_{\text{Stammfunktion}}\overbrace{\longrightarrow}^{\text{ableiten}} f(x)\overbrace{\longleftarrow}^{\text{integrieren}} \underbrace{f'(x)}_{\text{1.Ableitung}}\)
Hat man eine Funktion \(f(x)\) gegeben, so kann man das Integral der Funktion berechnen. Man erhält dann die sogenannte Stammfunktion \(F(x)\). Leitet man jedoch die Ausgangsfunktion \(f(x)\) ab, so erhält man die erste Ableitung der Funktion \(f'(x)\).
Leitet man die Stammfunktion \(F(x)\) ab, so gelangt man wieder zu der Ausgangsfunktion \(f(x)\). Integriert man die erste Ableitung \(f'(x)\), so gelangt man ebenfalls zur Ausgangsfunktion \(f(x)\)
Stammfunktion
Um einen vollständigen Überblick der Integralrechnung zu erhalten ist es wichtig, sich mit der Stammfunktion zu beschäftigen.
Eine Funktion \(F\) wird Stammfunktion der Funktion \(f\) genannt, wenn folgendes Gilt:
\(F'(x)=f(x)\)
für alle \(x\) im Definitionsbereich der Funktion \(f(x)\)
Die Ableitung der Stammfunktion \(F(x)\) ergibt die Funktion \(f(x)\).
Den Zusammenhang zwischen der Stammfunktion \(F(x)\) und der Funktion \(f(x)\) kann man auch in einer anderen Schreibweise finden:
Eine Andere Schreibweise
\(\begin{aligned} \frac{dF(x)}{dx}=f(x) \end{aligned}\)
Lasst euch von dieser Schreibweise nicht verwirren. Sollte euer Lehrer diese Schreibweise in der Integralrechnung und Differentialrechnung nicht verwenden, so müsst Ihr euch diese nicht merken.
Typische Stammfunktionen in der Integralrechnung
In der folgenden Tabelle sind einige typische Potenzfunktionen und ihre Stammfunktionen eingetragen.
| f(x) | F(x) |
| \(1\) | \(x\) |
| \(4\) | \(4\cdot x\) |
| \(x\) | \(\frac{1}{2}\)\(x^2\) |
| \(x^2\) | \(\frac{1}{3}\)\(x^3\) |
| \(2\cdot x^5\) | \(\frac{2}{6}\)\(x^6\) |
| \(x^2-4\) | \(\frac{1}{3}\)\(x^3-4\cdot x\) |
Wie dir womöglich aufgefallen ist, integriert man eine Potenzfunktion indem man den Exponenten um \(1\) erhöht und in den Nenner schreibt.
Regel
Integration von Potenzfunktionen
Die Stammfunktion zu der Pontenzfunktion
\(f(x)=x^n\)\(\,\,\,\,\,\,\,\,n\in\natnums\)
berechnet sich über:
\(F(x)=\)\(\frac{1}{n+1}\)\(x^{n+1}\)
Beispiel
Berechne die Stammfunktion von
\(f(x)=x^2+2x-1\)
Wir wenden die Regel zur Integration von Potenzfunktionen an und erhalten:
\(\begin{aligned} F(x)&=\frac{1}{3}x^3+\frac{2}{2}x^2-x\\ \\ &=\frac{1}{3}x^3+x^2-x \end{aligned}\)
Um zu überprüfen ob wir richtig integriert haben, können wir die Stammfunktion ableiten und sollten dann auf die Ursprungsfunktion kommen. Das liegt daran, weil das Ableiten die Umkehrung der Integration ist.
\(\begin{aligned} F'(x)&=\Big(\frac{1}{3}x^3+x^2-x\Big)'\\ \\ &=\frac{3}{3}x^2+2x-1\\ \\ &=x^2+2x-1 \end{aligned}\)
Wie du siehst haben wir die Stamfunktion korrekt ermittelt.
Bemerkung
Wir hätten zu unserer Stammfunktion eine beliebige Konstante addieren können ohne dabei eine falsche Stammfunktion zu erhalten.
\(\begin{aligned} F(x)&=\frac{1}{3}x^3+x^2-x+\underbrace{10}_\text{Konstante} \end{aligned}\)
Denn die Ableitung von \(F(x)\) mit der Konstanten würde immer noch zu unserer Ausgangsfunktion führen. Das liegt daran, dass die Konstante beim ableiten wegfällt.
Denn
\(10'=0\)
Allgemein schreibt man die Konstante in der Stammfunktion folgendermaßen:
\(\begin{aligned} F(x)=\frac{1}{3}x^3+x^2-x+C \end{aligned}\)
Der einfachheithalber lässt man die Konstante oft weg bzw. man setzt.
\(C=0\)
Wie du vielleicht bemerkt hast, gilt beim Integrieren die Summenregel. Eine Summe von Potenzfunktionen wird summandenweise integriert. Die gleiche Regel gibt es auch beim Ableiten von Funktion die aus Summen einzelner Faktoren besteht.
Weitere Beispiele zu typischen Stammfunktionen in der Integralrechnung
| f(x) | F(x) |
| \(e^x\) | \(e^x\) |
| \(3e^{3x}+1\) | \(e^{3x}+x\) |
| \(e^{2x}\) | \(\frac{1}{2}\)\(e^{2x}\) |
| \(e^{-2x}\) | \(-\frac{1}{2}\)\(e^{-2x}\) |
| \(\frac{1}{x}\) | \(ln(x)\) |
| \(\frac{1}{x^2}\) | \(-\frac{1}{x}\) |
| \(sin(x)\) | \(-cos(x)\) |
| \(cos(x)\) | \(sin(x)\) |
Wie du anhand der oberen Funktionen gesehen hast, ist das Integrieren von Funktion im Vergleich zum Ableiten etwas aufwendiger. Das liegt besonders daran, dass es weniger Integralregeln als beim Ableiten gibt. In der Differentialrechnung gibt es die Potenzregel, Faktorregel, Summenregel, Produktregel, Kettenregel und die Quotientenregel
In der Integralrechnung gibt es lediglich die Potenzregel, Faktorregel und die Partielle Integration.
Potenzregel
Die Stammfunktion zu der Pontenzfunktion
\(f(x)=x^n\)\(\,\,\,\,\,\,\,\,n\in\natnums\)
berechnet sich über:
\(F(x)=\)\(\frac{1}{n+1}\)\(x^{n+1}\)
Faktorregel
Die Stammfunktion zu der Funktion
\(f(x)=c\cdot g(x)\)
lautet
\(F(x)=c\cdot G(x)\)
Wobei \(c\) eine Konstante ist und \(G(x)\) die Stammfunktion von \(g(x)\) ist.
Unbestimmtes Integral
Das unbestimmte Integral dient als Bezeichung aller möglichen Stammfunktionen \(F(x)+C\) der Ausgangsfunktion \(f(x)\). Das unbestimmte Integral ist eine mathematische Schreibweise mit der man andeutet, dass man die Stammfunktion \(F(x)\) einer Funktion \(f(x)\) sucht. Die Schreibweise lautet:
\(\displaystyle\int f(x)\,\,\,dx=F(x)+C\)
Dabei ist das \(\displaystyle\int\) lediglich ein mathematisches Zeichen. Es hat zunächst keinen tieferen Sinn, mit diesem Zeichen möchte man dem Leser klar machen, das man eine Stammfunktion sucht. Um genau zu sein sucht man die Stammfunktion der Funktion \(f(x)\). Das Zeichen \(dx\) sagt einem, dass man die Funktion \(f(x)\) im Bezug auf die Variable \(x\) integrieren möchte.
Wir wissen ja bereits, dass eine Variable nur eine Platzhalter ist. Man kann eine Funktion begegnen, welche von der Variable \(y\) abhängt. Für das unbestimmte Integral würde man dann folgendes schreiben:
\(\displaystyle\int f(y)\,\,\,dy=F(y)+C\)
In diesem Fall ist die Integrationsvariable \(y\), weshalb man \(dy\) schriebt.
Beispiele:
- \(\displaystyle\int\,1\,\,\,dx=x+C\)
- \(\displaystyle\int\,x\,\,\,dx=\)\(\frac{1}{2}\)\(x^2+C\)
- \(\displaystyle\int\,3\cdot y^2\,\,\,dy=\)\(y^3+C\)
- \(\displaystyle\int\,e^{2x}\,\,\,dx=\)\(\frac{1}{2}\)\(e^{2x}+C\)
An der Art und Weise wie man eine Funktion integriert, ändert sich durch eine andere Integrationsvariable nichts. Die Rechenregeln der Integralrechnung bleiben gleich. Das \(dx\), \(dy\), etc. ist ledigleich ein Hinweis, mit dem uns mitgeteilt wird, nach welche Variable wir integrieren müssen.
Angenommen wir hätten eine Funktion die sowohl von \(x\) als auch von \(y\) abhängt:
\(f(x,y)=x\cdot y\)
und wir möchten die Stammfunktion im Bezug auf \(y\) berechnen. Dann würde das unbestimmte Integral wie folgt aussehen:
\(\begin{aligned} \displaystyle\int f(x,y)\,\,\,dy&=\displaystyle\int x\cdot y\,\,\,dy\\ \\ &=x \cdot \frac{y^2}{2} +C \end{aligned}\)
Wir haben also \(x\) wie eine Konstante behandelt und die Faktorregel für die Integration verwendet.
Mal angenommen wir möchten die gleiche Funktion nach \(x\) integrieren. Dann sehe das unbestimmte Integral wie folgt aus:
\(\begin{aligned} \displaystyle\int f(x,y)\,\,\,dx&=\displaystyle\int x\cdot y\,\,\,dx\\ \\ &=y \cdot \frac{x^2}{2} +C \end{aligned}\)
In diesem Fall haben wir \(y\) wie eine Konstante behandelt. Die Integrationsvariable \(dx\) hat uns mitgeteilt, dass die Variable \(y\) wie eine Konstante behandeln werden soll und die Integration lediglich im Bezug auf \(x\) durchgeführt werden muss.
Beispiel für unbestimmte Integrale
\(\displaystyle\int 2x\,\,\,dy=x^2+C\)
\(\displaystyle\int x^2\,\,\,dx=\frac{1}{3}x^3+C\)
\(\displaystyle\int 2+x\,\,\,dx=2x+\frac{1}{2}x^2+C\)
\(\displaystyle\int 1+y\,\,\,dy=y+\frac{1}{2}y^2+C\)
\(\displaystyle\int y^3\,\,\,dy=\frac{1}{4}y^4+C\)
Bestimmtes Integral
Für den vollständigen Überblick der Integralrechnung müssen wir noch das Thema bestimmtes Integral behandeln.
Der Unterschied zwischen einem unbestimmten und einem bestimmten Integral leigt darin, dass Integrationsgrenzen angegeben sind.
Man spricht von einem bestimmten Integral, wenn Integrationsgrenzen vorhanden sind.
\(\displaystyle\int^{b}_{a} f(x)\,\,\,dx\)
Hier ist die untere Grenze \(a\) und die obere Grenze ist \(b\).
Um ein bestimmtes Integral zu lösen muss man wie bei dem unbestimmten Integral die Stammfunktion bestimmen. Es kommt jedoch ein weiterer Schritt hinzu, bei dem man die Integrationsgrenzen in die Stammfunktion einsetzen muss.
Bestimmtes Integral
\(\displaystyle\int^{b}_{a} f(x)\,\,\,dx=\Big[F(x)\Big]^{b}_{a}=F(b)-F(a)\)
Man sollte sich von dem Zwischenschritt \(\Big[F(x)\Big]^{b}_{a}\) nicht verwirren lassen. Das ist ledigleich eine Schreibweise mit der man andeutet, dass die Integrationsgrenzen \(a,b\) in die Stammfunktion eingesetzt werden müssen.
Das bestimmte Integral kann auch lediglich wie folgt geschrieben werden:
\(\displaystyle\int^{b}_{a} f(x)\,\,\,dx=F(b)-F(a)\)
Der Zwischenschritt wird jedoch in der Schule von vielen Lehrern verwendet.
\(\Big[F(x)\Big]^{b}_{a}=F(b)-F(a)\)
Mit einem bestimmten Integral kann man die Fläche zwischen einer Funktion und der x-Achse berechnen. Dabei sind die Grenzen \(a\) und \(b\) die Grenzen der Fläche entlang der \(x\)-Achse.
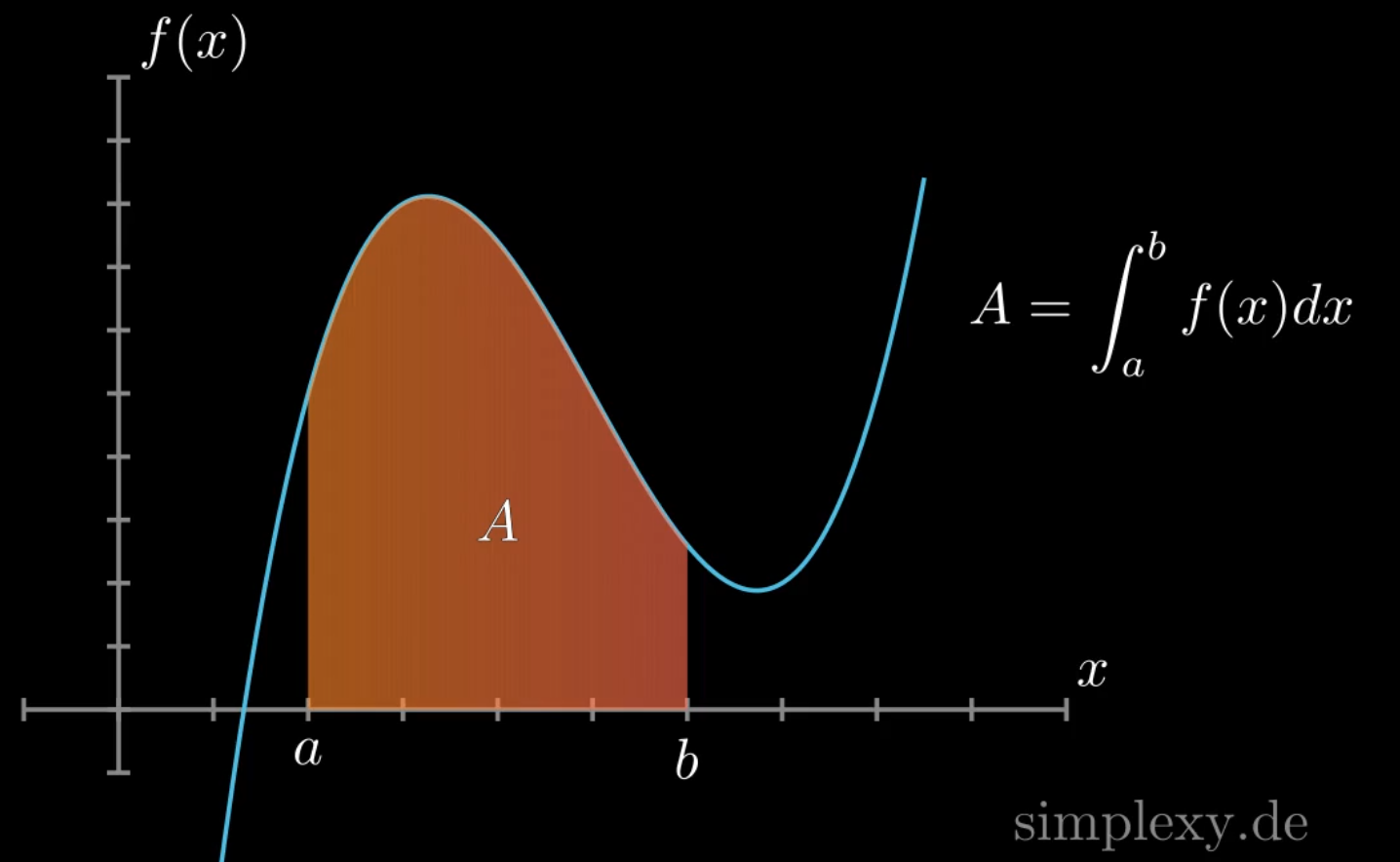
Fläche zwischen Funktion und der x-Achse berechnen mittels Integralrechnung
Mit dem bestimmten Integral kann man die Fläche zwischen einer Funktion und der \(x\)-Achse berechnen. Für einen vollständigen Überblick der Integralrechnung ist die dieses Theme sehr wichtig. Es wird in der Schule im Zusammenhang mit der Integralrechnung behandeln und kommt meistens in den Abitur-Klausuren ran.
Beispiel 1
Wie groß ist die Fläche die vom Graphen der Funktion
\(f(x)=-(x-3)^2+4\)
und der \(x\)-Achse im Intervall \([1,5]\) eigeschlossen wird?
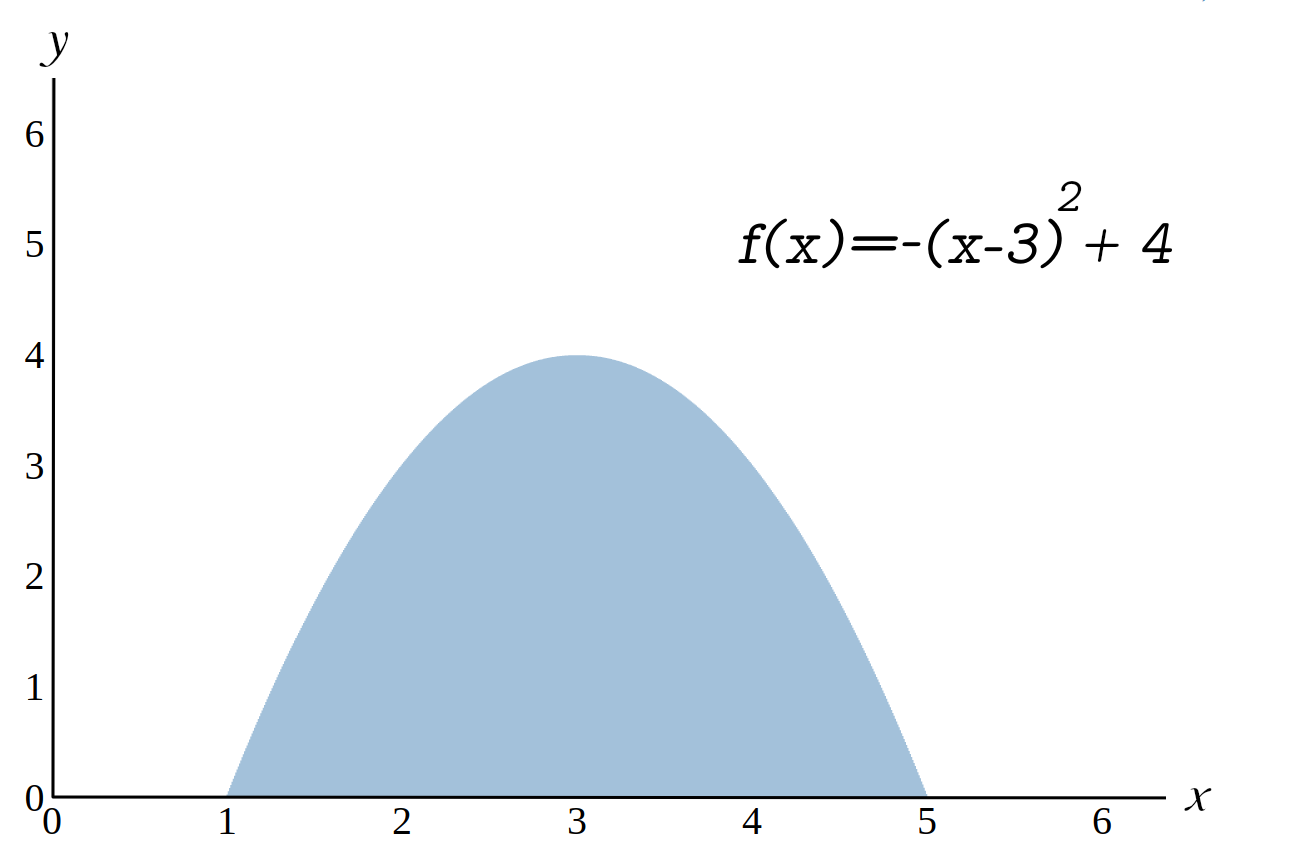
Lösung
Wir erhalten die Fläche zwischen der Funktion und der \(x\)-Achse, indem wir das bestimmte Integral mit der unteren Grenze \(1\) und der oberen Grenze \(5\) berechnen.
\(\displaystyle\int^{5}_{1} -(x-3)^2+4\,\,\,dx=\)\(\Big[-\)\(\frac{1}{3}\)\(x^3+3x^2-5x\Big]^{5}_{1}\)
\(\,\,=\Big(\)\(-\frac{1}{3}\)\(5^3+3\cdot 5^2-5\cdot 5\Big)-\)\(\Big(\)\(-\frac{1}{3}\)\(1^3+3\cdot 1^2-5\cdot 1\Big)\)
\(\,\,=8,33+2,33=10,66\,\,FE\)
Die Fläche unter dem Graphen im Intervall \([1,5]\) ist \(10,66\) Flächeneinheiten groß.
Beispiel 2
Wie groß ist die Fläche zwischen der Funktion
\(f(x)=-x^2+1\)
und der \(x\)-Achse.
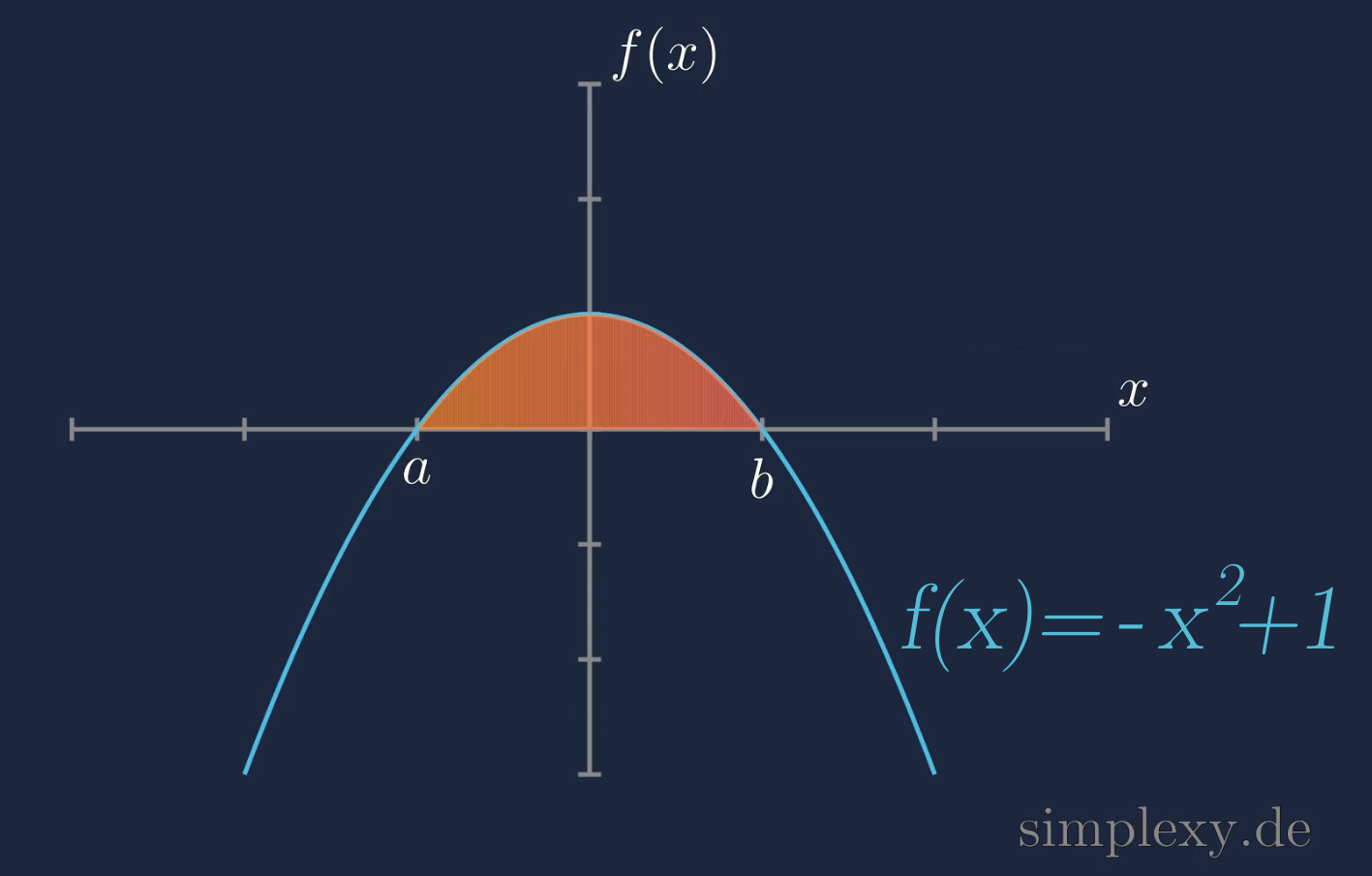
Lösung
Uns fällt auf, das uns keine Integrationsgrenzen gegeben sind. Wir müssen die Integrationsgrenzen selber bestimmen. Wir haben es hier mit einer umgedrehten Parabel zu tun. Diese Parabel besitzt zwei Nullstellen, die Linke Nullstelle wäre die untere Grenze und die Rechte Nullstelle wäre die obere Grenze. Wir müssten als erstes die Grenzen des bestimmten Integrals berechen. Das Können wir machen, indem wir die Nullstellen der Parabel berechnen.
Mit der pq-Formel berechnen wir die Nullstellen von
\(f(x)=-x^2+1\)
und erhalten die Nullstellen
\(x_1=-1\) und \(x_2=1\)
Die untere Grenze ist also \(-1\) und die obere Grenze ist \(1\). Die Fläche unter der Funktion erhalten wir über das bestimmte Integral
\(\displaystyle\int^{1}_{-1} -x^2+1\,\,\,dx=[-\frac{1}{3}x^3+x]^{1}_{-1}=\frac{2}{3}+\frac{2}{3}=\frac{4}{3}\)
Die Fläche zwischen dem Graphen und der \(x\)-Achse beträgt \(\frac{4}{3}\) Flächeneinheiten.
Beispiel 3
Bestimme die Fläche zwischen dem Graphen der Funktion
\(f(x)=x^3\)
und der \(x\)-Achse im Intervall \([-1,1]\).
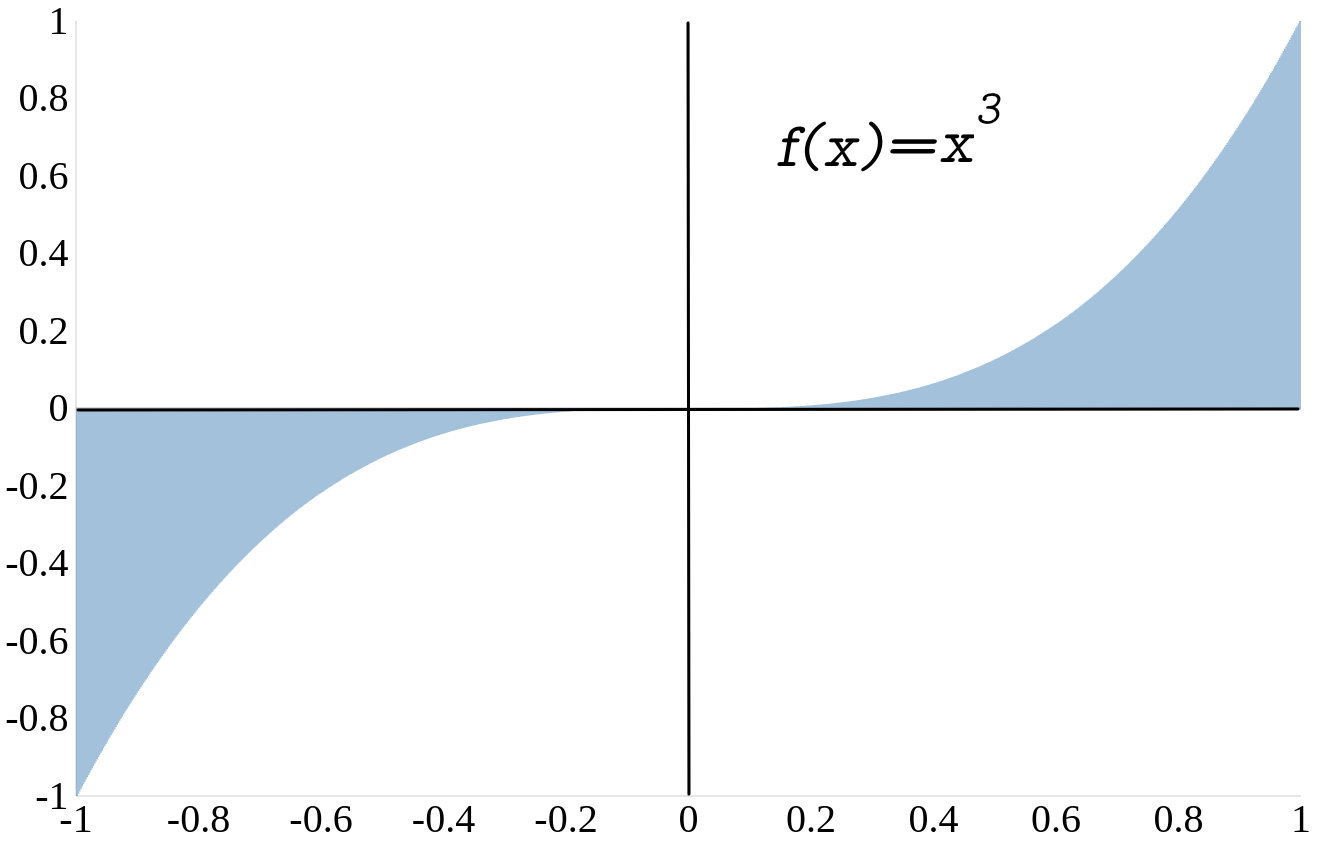
Lösung
Um die Fläche unter dem Graphen zu erhalten müssen wir das folgende bestimmte Integral lösen:
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx\)
Achtung !
In diesem Fall liegt ein Teil der Fläche unterhalb der x-Achse. Das bestimmte Integral in dem Intervall \([-1,0]\) würde eine negative Zahl ergeben. Da eine Fläche nicht negativ sein kann, müssen wir den Betrag dieser negativen Zahl berechnen.
Da der Graph der Funktion \(f(x)=x^3\) im Intervall \([-1,0]\) unterhalb der \(x\)-Achse liegt, müssen wir das bestimmte Integral in zwei Teile spalten:
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx=\displaystyle\int^{0}_{-1} x^3\,\,\,dx+\displaystyle\int^{1}_{0} x^3\,\,\,dx\)
Nun müssen wir beachten, dass das bestimmte Integral im Intervall \([-1,0]\) eine negative Zahl ergibt.
\(\displaystyle\int^{0}_{-1} x^3\,\,\,dx=\big[\frac{1}{4}x^4\big]_{-1}^{0}=-\frac{1}{4}\)
Die Fläche zwischen \(x\)-Achse und der Funktion im Intervall \([-1,0]\) beträgt
\(\begin{aligned} |-\frac{1}{4}|=\frac{1}{4} \end{aligned}\)
Wir haben hier den Betrag von \(-\frac{1}{4}\) berechnet. Der Betrag einer negativen Zahl ist die gleiche Zahl nur positiv.
Nun müssen wir noch den zweiten Teil des bestimmten Integrals im Intevall \([0,1]\) berechnen:
\(\displaystyle\int^{1}_{0} x^3\,\,\,dx=\big[\frac{1}{4}x^4\big]_{0}^{1}=\frac{1}{4}\)
Insgesammt erhalten wir für die Fläche:
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
Die Fläche zwischen der Funktion und der \(x\)-Achse beträgt \(\frac{1}{2}\) Flächeneinheiten.
Achtung !
Es ist sehr wichtig das man sich ein Bild von der Funktion macht. Nur so weis man ob ein Teil der Funktion unterhalb der x-Achse liegt. Würde man hier das bestimmte Integral ausrechnen ohne es in zwei Teil zu spalten, würde als Ergebniss Null rauskommen.
\(\displaystyle\int^{1}_{-1} x^3\,\,\,dx=0\)
Aus unserer Rechnung wissen wir aber, das die Fläche zwischen der Funktion \(f(x)=x^3\) und der \(x\)-Achse im Intervall \([-1,1]\) gleich \(\frac{1}{2}\) Flächeneinheiten groß ist.
Bestimmtes Integral Aufteilen
Ein bestimmtes Integral kann aufgeteilt werden, indem man die Intervallgrenzen aufteilt.
\(\displaystyle\int^{c}_{a} f(x)\,\,\,dx=\displaystyle\int^{b}_{a} f(x)\,\,\,dx+\displaystyle\int^{c}_{b} f(x)\,\,\,dx\)
Beispiel 4
Berechne die Fläche \(A\) zwischen dem Graphen der Funktion
\(f(x)=-\frac{1}{2}x^2+3x-\frac{5}{2}\)
Lösung
Wir müssen wieder die Intervallgrenzen bestimmen. Dazu brauchen wir die Nullstellen der Funktion.
Mit der Mitternachtsformel erhalten wir die zwei Nullstellen
\(x_1=1\)
und
\(x_2=5\)
Nun können wir diese zwei Nullstellen als Intervallgrenzen für das bestimme Integral verwenden:
\(\begin{aligned} A&=\displaystyle\int^{5}_{1} -\frac{1}{2}x^2+3x-\frac{5}{2}\,\,\,dx\\ \\ &=\Big[-\frac{1}{6}x^3+\frac{3}{2}x^2-\frac{5}{2}x\Big]_{1}^{5}=\frac{16}{3} FE \end{aligned}\)
Beispiel 5
Für die Funktion
\(f(z)=-z^3+6z^2-8z\)
soll die Fläche \(A\) zwischen dem Graphen der Funktion und der z-Achse im Intervall \([1,3]\) berechnet werden.
Lösung
Als Erstes müssen wir von der Funktion \(f(z)\) die Nullstellen berechnen. Diese Lauten:
\(z_1=0\) und \(z_2=2\) und \(z_3=4\)
Achtung
Die Nullstelle \(z_3=4\) befindet sich nicht im Intervall \([1,3]\).
Da sich die Dritte Nullstelle \(z_3=4\) der Funktion \(f(z)\) nicht im Intervall \([1,3]\) befindet, ergibt sich folgendes bestimmte Integral
\(\begin{aligned} A&=\Bigg|\displaystyle\int^{3}_{1} -z^3+6z^2-8z\,\,\,dz\Bigg|\\ \\ &=\Bigg|\displaystyle\int^{2}_{1} -z^3+6z^2-8z\,\,\,dz\Bigg|+\Bigg|\displaystyle\int^{3}_{2} -z^3+6z^2-8z\,\,\,dz\Bigg|\\ \\ &=\Bigg|\Bigg[-\frac{1}{4}z^4+2z^3-4z^2\Bigg]_1^2\Bigg|+\Bigg|\Bigg[-\frac{1}{4}z^4+2z^3-4z^2\Bigg]_2^3\Bigg|\\ \\ &=\Big|-\frac{7}{4}\Big|+\Big|\frac{7}{4}\Big|\\ \\ &=\frac{7}{2}\,\,\,\text{FE} \end{aligned}\)
Die Fläche zwischen der Funktion \(f(z)\) und der z-Achse im Intervall von \([1,3]\) beträgt \(\frac{7}{2}\) Flächeneinheiten.
Fläche zwischen zwei Funktionen
Beispiel 6
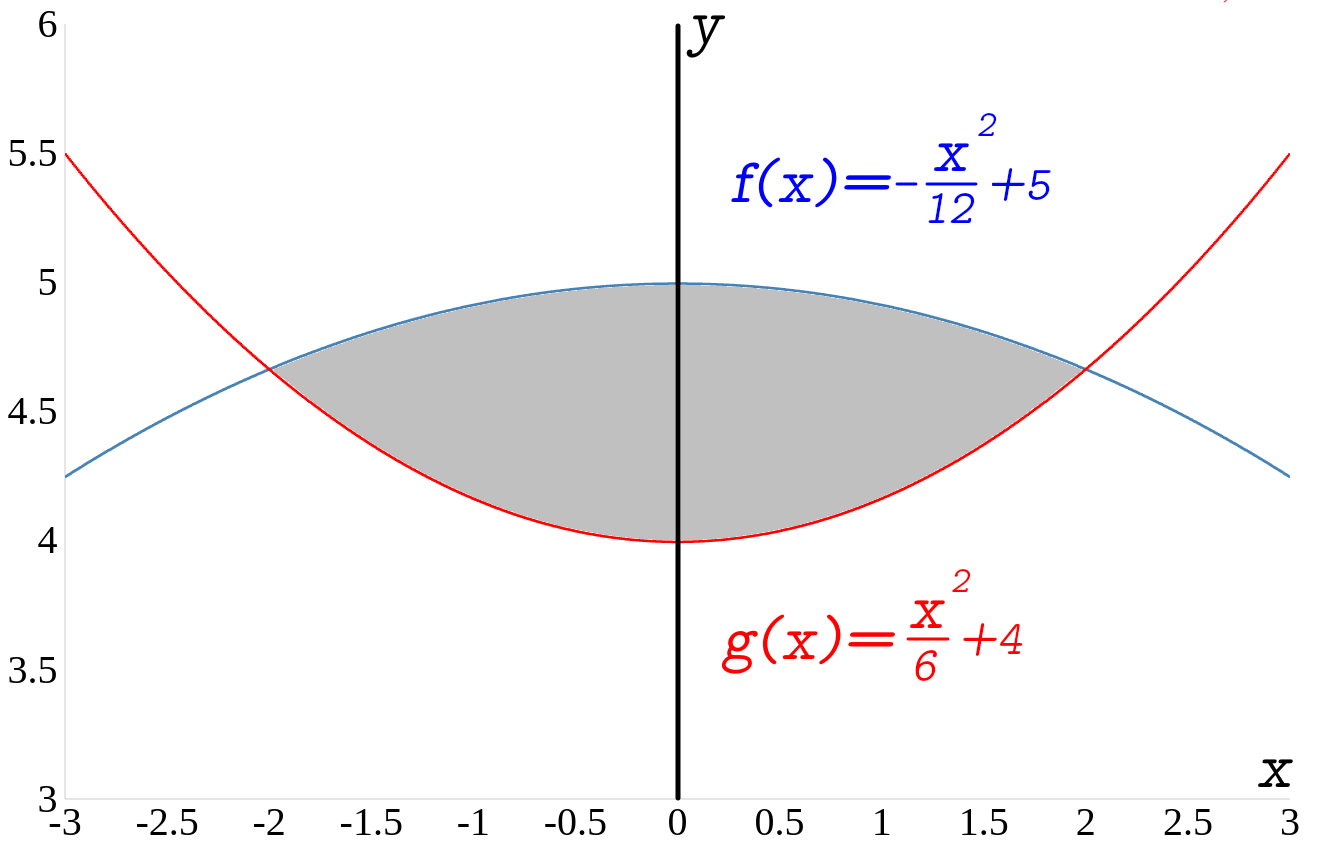
Wie groß ist die Fläche \(A\) zwischen den zwei folgenden Funktionen.
\(\begin{aligned} f(x)=-\frac{x^2}{12}+5 \end{aligned}\)
und
\(\begin{aligned} g(x)=\frac{x^2}{6}+4 \end{aligned}\)
In der unteren Abbildung sind beide Funktion und die eingeschlossene Fläche dargestellt.
vorgehensweise
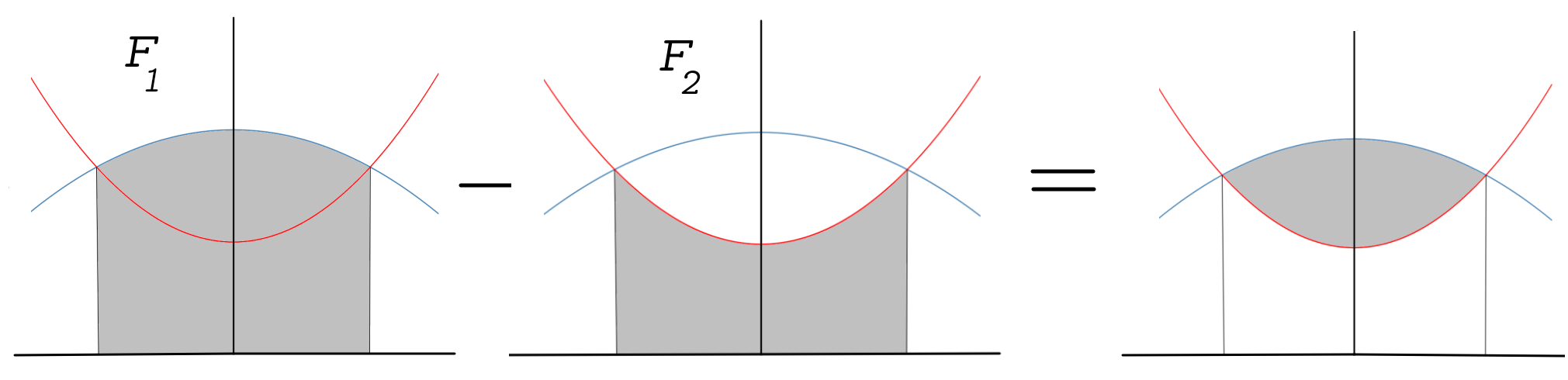
- Zunächst müssen die Schnittpunkte \(x_1\) und \(x_2\) der zwei Funktionen Berechnet werden.
- Anschließend wird die Fläche zwischen der \(x\)-Achse und der Funktion \(f(x)\) im Intervall \([x_1,x_2]\)berechnet. Nennen wir diese Fläche \(F_1\).
- Dann benötigt man noch die Fläche zwischen der Funktion \(g(x)\) und \(x\)-Achse im Intervall \([x_1,x_2]\). Diese Fläche nennen wir \(F_2\).
- Um die Fläche zwischen den zwei Funktionen zu bekommen müssen wir die Flächen \(F_1\) und \(F_2\) von einander abziehen, also \(F_1-F_2\) berechnen.
Lösung
Um die Fläche zwischen zwei Funktionen zu berechnen müssen wir zunächst die Schnittpunkte der zwei Funktionen berechnen. Dazu setzen wir beide Funktionen gleich und stellen die Gleichung nach \(x\) um. Da die Funktionen \(f(x)\) und \(g(x)\) Parabeln sind, werden wir zwei Schnittpunkte \(x_1\) und \(x_2\) erhalten.
\(\begin{aligned} -\frac{x^2}{12}+5&=\frac{x^2}{6}+4\\ \\ &\implies\\ \\ x_1=2\,\,\,&\text{und}\,\,\,x_2=-2 \end{aligned}\)
Wir Können nun die Fläche \(F_1\) zwischen der Funktionen \(f(x)\) und der x-Achse im Intervall \([-2,2]\) berechnen.
\(\begin{aligned} F_1&=\displaystyle\int^{2}_{-2} -\frac{x^2}{12}+5=\frac{176}{9}\,\,\text{FE} \end{aligned}\)
Nun berechnen wir noch die Fläche \(F_2\) zwischen der Funktion \(g(x)\) und der x-Achse im Intervall \([-2,2]\)
\(\begin{aligned} F_2&=\displaystyle\int^{2}_{-2} \frac{x^2}{6}+4=\frac{152}{9}\,\,\text{FE} \end{aligned}\)
Um die Fläche zwischen den zwei Funktionen zu erhalten müssen wir nun die zwei Teilflächen \(F_1\) und \(F_2\) von einander abziehen.
\(\begin{aligned} A&=F_1-F_2\\ \\ &=\frac{176}{9}\,\,\text{FE}-\frac{152}{9}\,\,\text{FE}\\ \\ &=\frac{8}{3}\,\,\text{FE} \end{aligned}\)
Die Fläche zwischen den zwei Funktionen \(f(x)\) und \(g(x)\) beträgt \(\frac{8}{3}\) FE.
Diese Vorgehensweise kann man für beliebige Funktionen wie folgt verallgemeinern.
Fläche zwischen zwei sich schneidenen Graphen
Wenn \(f\) und \(g\) zwei Funktionen sind, die im Intervall \([a,b]\) stetig sind und \(f(x)\geq g(x)\) für alle \(x\) in diesem Intervall. Dann berechnet sich die Fläche zwischen den zwei Graphen über die folgende Formel:
\(\begin{aligned} A&=\displaystyle\int^{b}_{a}\Big(f(x)-g(x)\Big)\,\,\,dx=\Big[F(x)-G(x)\Big]_a^b\\ \\ &=\Big(F(b)-G(b)\Big)-\Big(F(a)-G(a)\Big) \end{aligned}\)
Wurzelfunktion Integrieren
\(\begin{aligned} f(x)&=\sqrt{x}\\ \\ F(x)&=\frac{2}{3}x^{\frac{3}{2}} \end{aligned}\)
e-Funktion integrieren
Das Integral der \(e\)-Funktion ist wieder die \(e\)-Funktion.
Regel:
\(\underbrace{F(x)=e^{x}}_{\text{Stammfunktion}}\overbrace{\leftarrow}^{\text{integrieren}} f(x)=e^{x}\overbrace{\rightarrow}^{\text{ableiten}} \underbrace{f'(x)=e^{x}}_{\text{1.Ableitung}}\)
\(e^{-x}\) Integrieren
Möchte man die Funktion \(e^{-x}\) integrieren, so muss beachtet werden, dass sich im Exponenten zusätzlich zum \(x\) noch ein Minus befindet.
Leiten wir mal zur Probe die Funktion \(f(x)=e^{-x}\) ab:
\(f'(x)=-e^{-x}\)
Das Minus ist aus dem Exponenten nach unten gekommen.
Nun Fragen wir uns, welche Funktion müssen wir ableiten um \(e^{-x}\) zu erhalten?
Die Antwort wäre:
\(F(x)=-e^{-x}\)
Wir können eine Probe machen und die Stammfunktion \(F(x)\) ableiten:
\(F'(x)=-(-e^{-x})'=e^{-x}\)
Die Stammfunktion von \(e^{-x}\) ist somit \(-e^{-x}\).
Berechnet man das Integral einer Funktion, kann man sich die Frage stellen,
"Welche Funktion muss ich ableiten um auf die gegebene Funktion zu kommen?"
Beim Integrieren der \(e\)-Funktion muss darauf geachtet werden ob im Exponenten nur ein \(x\) steht oder nicht. Wenn im Exponenten mehr als nur ein \(x\) steht, so muss man eventuell die Integration mittels Substitution durchführen.
\(\begin{aligned} f(x)&=e^{-x}\\ \\ F(x)&=-e^{-x} \end{aligned}\)
Logarithmus Funktion integrieren
Regel
Integral der Logarithmus-Funktion
\(\displaystyle\int ln(x)\,dx=ln(x)\cdot x-x\)
Das Integral der Logarithmus Funktion ist etwas schwerer. Für die Herleitung kann man Hier Clicken,
Sinus Funktion Integrieren
\(\begin{aligned} f(x)&=sin(x)\\ \\ F(x)&=-cos(x) + C \end{aligned}\)
Regel
Stammfunktion von Sinus
Die Stammfunktion vom Sinus ergibt die Minus Cosinus Funktion.
Integral von \(f(x)=sin(x)\) ergibt:
\(\displaystyle\int sin(x)\,dx =-cos(x) + C \)
\(F(x)=-cos(x) + C \)
Dabei ist \(C\) eine beliebige Konstante.
Cosinus Funktion Integrieren
Die Stammfunktion vom Cosinus ist der Sinus.
\(\begin{aligned} f(x)&=cos(x)\\ \\ F(x)&=sin(x) + C \end{aligned}\)
Regel
Stammfunktion von Cosinus
Die Stammfunktion vom Cosinus ergibt die Sinus Funktion.
Integral von \(f(x)=cos(x)\) ergibt:
\(\displaystyle\int cos(x) dx =sin(x) + C \)
\(F(x)=sin(x) + C \)
Dabei ist \(C\) eine beliebige Konstante.
Partielle Integration
Die partielle Integration ist in der Integralrechnung eine Möglichkeit, mit der man Stammfunktionen bestimmen kann und Integrale lösen kann.
Regel:
Partielle Integration Formel
\(\displaystyle\int_a^b f'(x)g(x)\,\,dx = \Big[f(x)g(x)\Big]_a^b-\displaystyle\int_a^b f(x)g'(x)\,\,dx\)
Die partielle Integration wird manchmal auch als Produktintegration bezeichnet. Denn diese Art der Integralrechnung wird stets angewandt, wenn man ein Produkt zweier Funktionen integrieren muss. Dabei ist es wichtig, dass man die Stammfunktion einer der beiden Funktion kennt (\(f'(x)\)) und das Integral durch die Ableitung der anderen Funktion \(g(x)\) leichter wird.
Die partielle Integration trägt das Wort "partielle" in sich, weil ein Teil des Integrals
\(\Big[f(x)g(x)\Big]\)
gelöst wird und der andere Teil
\(\displaystyle\int f(x)g'(x)\,\,dx\)
noch ein Integral beinhaltet.
Die Herausforderung bei der partiellen Integration liegt darin, herauszufinden welchen Teil man als \(f'(x)\) und welchen man als \(g(x)\) auffassen muss. Man muss sich also immer die Frage stellen:
Die Ableitung von welchem Faktor vereinfacht das Integral?
Beispiel
Berechne die Stammfunktion der folgenden Funktion
\(h(x)=x\cdot e^x\)
Lösung
Die Stammfunktion berechnet sich über das unbestimmte Integral
\(\displaystyle\int x\cdot e^x\,\,dx\)
Wir können die Stammfunktion nicht so einfach berechnen wie in den letzten Beispielen. Wir haben es hier mit einem Produkt aus zwei Funktionen zu tun. Wir können dieses Integral mit Hilfe der partiellen Integration lösen. Definieren wir die folgenden Funktionen:
\(f'(x)=e^x\)
und
\(g(x)=x\)
Das Integral kann nun mittels dieser zwei Funktion ausgedrückt werden:
\(h(x)=x\cdot e^x=g(x)\cdot f'(x)\)
Das unbestimmte Integral wird zu:
\(\displaystyle\int x\cdot e^x\,\,dx=\displaystyle\int g(x)\cdot f'(x)\,\,dx\)
Nun können wir die Formel der partiellen Integration anwenden:
\(\begin{aligned} \displaystyle\int f'(x)g(x)\,\,dx &= f(x)g(x)-\displaystyle\int f(x)g'(x)\,\,dx\\ \\ &=\underbrace{e^x}_{f(x)}\cdot \underbrace{x}_{g(x)}-\displaystyle\int \underbrace{e^x}_{f(x)}\cdot\underbrace{1}_{g'(x)}\,\,dx\\ \\ &=e^x\cdot x-\displaystyle\int e^x\,\,dx\\ \\ &=e^x\cdot x-e^x \end{aligned}\)
Als Lösung erhalten wir also
\(\displaystyle\int x\cdot e^x\,\,dx=e^x\cdot x-e^x\)
Das gleiche geht natürlich auch für den Fall das man ein bestimmes Integral lösen muss.
Es ist sehr wichtig das man erkennt welche der zwei Faktoren der Ausgangsfunktion als \(f'(x)\) und welche als \(g(x)\) bezeichnet werden muss. Ansonten kann es vorkommen, dass man das Integral nicht lösen kann. Würde man in dem oberen Beispiel \(f'(x)=x\) und \(g(x)=e^x\) verwenden, so könnte man das Integral nicht lösen. Sollte man beim Lösen eines Integrals mittels partieller Integration nicht weiter kommen, kann es hilfreich sein die Aufgabe zu wiederholen und \(f'(x)\) und \(g(x)\) zu vertauchen.
Hinweis
Manchmal muss man die partielle Integration zwei mal oder mehrmals anwenden.
Potenzen \(x^n\) und Umkehrfunktionen (ln, arcsin, arccos, etc.) werden durch Ableiten einfachen. Daher werden diese oft als \(g(x)\) gewählt. Funtionen wie die Exponentialfunktion \(e^x\) oder die Sinusfunktion \(sin(x)\) werden duch das Ableiten komplizierter und sollte daher als \(f'(x)\) gewählt werden.
Andere Schreibweise der partiellen Integration
\(\displaystyle\int_a^b u(x)v'(x)\,\,dx = \Big[u(x)v(x)\Big]_a^b-\displaystyle\int_a^b u'(x)v(x)\,\,dx\)
Herleitung der Stammfunktion des natürlichen Logarithmus mittels partielle Integration
In der Integralrechnung muss man oft mit der Logarithmus Funktion hantieren. Wir werden daher nun die partielle Integration verwenden, um die Stammfunktion der Logarithmus Funktion zu berechnen.
\(\displaystyle\int ln(x)\,dx=\displaystyle\int 1\cdot ln(x)\,dx\)
Der erste Schritt ist ein Trick, der in der Mathematik oft Anwendung findet. Wir haben zu \(ln(x)\) eine Mltiplikation mit \(1\) hinzugefügt. Dieser Trick ermöglicht nun die Anwendung der partiellen Integration. Dazu nehmen wir folgende Bezeichnung vor:
\(f'(x)=1\implies f(x)=x\)
\(g(x)=ln(x)\implies g'(x)=\frac{1}{x}\)
Nun wenden wir die Formel der partiellen Integration an:
\(\displaystyle\int f'(x)g(x)\,\,dx = f(x)g(x)-\displaystyle\int f(x)g'(x)\,\,dx\)
\(\displaystyle\int 1\cdot ln(x)\,dx=x\cdot ln(x)-\underbrace{\displaystyle\int x\cdot \frac{1}{x}\,dx}_{\displaystyle\int 1\,dx =x}\)
\(\implies \displaystyle\int ln(x)\,dx=x\cdot ln(x)-x\)
Die Stammfunktion der ln-Funktion lautet also:
\(x\cdot ln(x)-x\)
Wir haben also mittels partieller Integration die Stammfunktion der ln-Funktion berechnen können. Dabei haben wir eine Multipliktion mit \(1\) eingeschoben, dieser Trick ist hilfreich und kommt anderweitig in der Mathematik vor.
Integration durch Substitution
Ein weiterer wichtiger Bestandteil der Integralrechnung ist die Integration durch Substitution. Unter einer Substitution versteht man in der Mathematik, dass Ersetzen eines Terms durch einen anderen oder das Umbenennen eines Terms um ihn zu vereinfachen.
In der Integralrechnung verwendet man die Substitution um eine neue Integrationsvariable einzuführen. Dadurch wird ein Teil des Integranden ersetzt und das Integral wird vereinfacht. Durch eine Substitution kann man ein Integral auf ein anderes bekanntes Integral zurückführen oder das Integral in ein einfacheres Integral umwandeln.
Integration durch substitution
\(\displaystyle\int_a^b f(u(x))\cdot u'(x)\,dx=\displaystyle\int_{u(a)}^{u(b)} f(u)\,du\)
Die Integration durch Substitution ist hilfreich, dort wo ein Faktor im Integranden gerade die Ableitung eines anderen Teils des Integranden ist. Das wird am besten deutlich mit Hilfe der folgenden Beispiele:
Beispiele 1
\(\displaystyle\int 2x\cdot e^{x^2}\,dx\)
Durch scharfes Hinsehen, erkennen wir das im Exponenten der e-Funktion der Term \(x^2\) steht, die Ableitung \((x^2)'=2x\) steht aber auch als Faktor vor dem \(e^{x^2}\). Man kann den Integranden folgendermaßen umschreiben bzw. substituieren:
\(u=x^2\)
\(\frac{du}{dx}=2x\implies dx=\frac{1}{2x}\,\,du\)
Wir können nun \(dx\) im Integral erstezen mit
\(\frac{1}{2x}\,\,du\)
Das Integral wird zu
\(\displaystyle\int 2x\cdot e^{x^2}\,\frac{1}{2x}\,du=\displaystyle\int e^{x^2}\,du\)
Jetzt erstezen wir noch \(x^2\) mit \(u\) und erhalten:
\(\displaystyle\int e^{u}\,du\)
Durch die Substiontion \(x^2=u\) ist es uns gelungen, dass komplizierte Integral in ein sehr einfaches Integral umzuwandeln.
Wir müssen als nun das folgende Integral lösen:
\(\displaystyle\int e^{u}\,du\)
Wir wissen aber was die Lösung dieses Integrals ist, es handelt sich lediglich um die Integration der e-Funktion.
\(\displaystyle\int e^{u}\,du=e^u+c\)
Jetzt müssen wir nur noch die Rücksubstitution durhführen, bei der man \(u\) wieder in \(x^2\) umschreibt.
\(e^{u}+c\rightarrow e^{x^2}+c\)
Damit haben wie die entgültige Lösung des Ausgangsintegrals ermittelt
\(\displaystyle\int 2x\cdot e^{x^2}\,dx=e^{x^2}+c\)
Bei der Substitution wird eine neue Integrationsvariable eingeführt, die das Integral leichter macht oder auf ein bekanntes Integral zurückführt.
Vorgehen beim Integrieren durch Substitution:
- Analysiere das Integral.
- Bestimmte die innere Funktion \(u(x)\).
- Berechne die Ableitung von \(u\) nach \(x\), also \(\frac{du(x)}{dx}\) und forme das nach \(dx\) um.
- Ersetze im Ausgangsintegral die innere Funktion mit \(u(x)\) und ersetze das \(dx\).
- Berechne die Stammfunktion der substituierten Funktion.
- Führe die Rücksubstitution durch, bei der du \(u(x)\) wieder mit dem Term aus Schritt 2 ersetzt.
Beispiele 2
Finde durch anwenden der Substitutionsregel die Lösung für das folgende Integral:
\(\displaystyle\int 2x\cdot (x^2+1)^4\,dx\)
Zunächst einmal muss man sich das Integral genau angucken und analysieren. Wir erkennen den Term \(x^2+1\) und sehen dass die Ableitung von diesem Term, also
\((x^2+1)'=2x\)
ebenfalls als Vorfaktor im Integranden vorkommt. Der erste Schritt bei der Partiellen Integration besteht meist darauß zu erkennen ob im Integral sowohl ein Term als auch seine Ableitung vorkommt.
Wir nennen nun die innere Funktion \(u(x)\):
\(u(x)=x^2+1\)
Nun besimmten wir die Ableitung von \(u(x)\):
\(\begin{aligned} u'(x)=\frac{du}{dx}=2x \implies dx=\frac{1}{2x}\cdot du \end{aligned}\)
Wir ersetzen nun im Ausgangsintegral die innere Funktion mit \(u\) und ersetzen das \(dx\) mit \(\frac{1}{2x}\cdot du\).
\(\begin{aligned} \displaystyle\int 2x\cdot (x^2+1)^4\,dx &= \displaystyle\int 2x\cdot u^4\frac{1}{2x}\,du\\ \\ &=\displaystyle\int u^4\,du=\frac{1}{5}u^5 \end{aligned}\)
Wir haben das Integral durch die Substitution in ein einfaches Integral einer Potenzfunktion zurückgeführt und gelöst.
Als letztes müssen wir die Rücksubstitution durchführen, bei dem wir für \(u\) wieder \(x^2+1\) ersetzen.
\(\frac{1}{5}u^5=\frac{1}{5}(x^2+1)^5\)
Damit haben wir unser Integral gelöst:
\(\displaystyle\int 2x\cdot (x^2+1)^4\,dx=\frac{1}{5}(x^2+1)^5\)
Sonderfälle
Lineare Substitution
Hat die innere Funktion von \(f\) die Form einer Linearen Funktion, so kann man folgende Regel anwenden:
\(\displaystyle\int_a^b f(mx+n)\,dx=\frac{1}{m}\big[F(mx+n)\big]_a^b\)
Logarithmische Integration
Ist der Integrand ein Bruch, bei dem der Zähler die Ableiten des Nenners ist, so kann man folgende Regel anwenden:
\(\begin{aligned} \displaystyle\int_a^b\frac{g'(x)}{g(x)}\,dx=\big[ln(|g(x)|)\big]_a^b \end{aligned}\)
Mittelwertsatz der Integralrechnung
Die Integralrechnung wird nicht nur verwendet um Flächen unter einem Graphen zu berechnen. Je nach Sachverhalt wird die Integralrechnung verwendet, um die verschiedensten Größen zu ermitteln.
Mit dem Mittelwertsatz der Integralrechnung kann man den Mittelwert einer Größe in abhängigkeit von einer anderen Größe berechnen. Muss man beispielsweise die mittlere Wassermenge bestimmten, die in einem bestimmten Zeitraum in ein Becken fließt, so bedient man sich oft an dem Mittelwertsatz.
Mittelwertsatz der Integralrechnung
\(\begin{aligned} \frac{1}{b-a}\displaystyle\int_a^b f(x)\,dx&=\frac{1}{b-a}\big[F(x)\big]_a^b=\frac{1}{b-a}\big(F(b)-F(a)\big) \end{aligned}\)
Dabei ist der Mittelwert gerade der Durchschnitt aller y-Werte einer Größe.
Es ist sehr wichtig, dass man auf die Achsen achtet und darauf was die gegebene Funktion im Sachverhalt angibt.
Beispiele
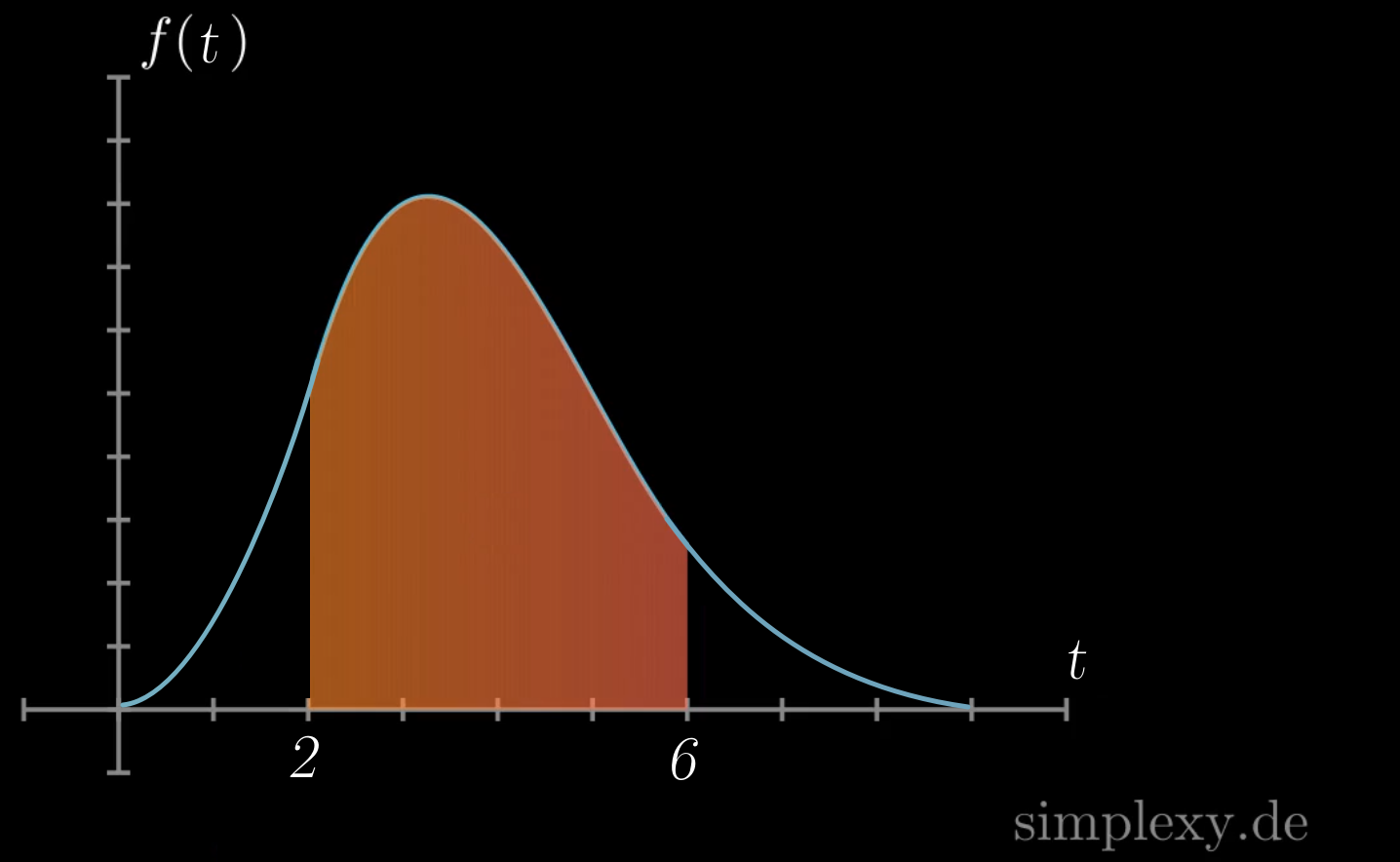
In der oberen Abbildung stellt \(f(t)\) den Wasserstand in einem Becken wieder. Der Wasserstand im Becken ist offensichlich zu unterschiedlichen Zeiten unterschiedlich hoch. Möchte jemand die durchschnittliche Höhe des Wasserstandes im Zeitraum von \(t=2\) stunden und \(t=6\) stunden haben, so kann man den Mittewertsatz der Integralrechnung anwenden.
\(\begin{aligned} \frac{1}{6-2}\displaystyle\int_2^6 f(t)\,dt \end{aligned}\)
\(=\) durchschnittliche Höhe des Wasserstandes im angegebenen Zeitraum.
Die Funktion \(f(t)\) aus der oberen Abbildung könnte in einem anderen Sachverhalt, die Fließgeschwindigkeit des Wasser in ein Becken darstellen. Man könnte als nun die durchschnittliche Zunahmegeschwindigkeit des Wassers in dem Zeitraum von \(t=2\) und \(t=6\) stunden berechnen.
\(\begin{aligned} \frac{1}{6-2}\displaystyle\int_2^6 f(t)\,dt \end{aligned}\)
\(=\) durchschnittliche Zunahmegeschwindigkeit des Wassers in dem Zeitraum.
Je nachdem was für einen Sachverhalt man gerade betrachtet, kann der Mittelwertsatz der Integralrechnung verwendet werden um einen bestimmten Durchschnittswert zu berechnen.
Uneigentliches Integal
Trifft man in der Integralrechnung ein Integral bei dem eine Grenze vorgegeben ist und die andere ist unendlich (\(\infty\)), so spricht man von einem uneigentlichen Integral.
\(\displaystyle\int_a^\infty f(x)\,dx\)
Hier muss man mit dem Grenzwertsatz \(\big(lim\big)\) arbeiten um das Integral zu lösen. Konvergiert die Funktion im Unendlichen gegen einen bestimmten Wert, so ist das Integral lösbar. Man sagt, das Integral Konvergiert. Hat man jedoch eine Funktion, die im Unendlichen divergiert, so wird auch das uneigentliche Integral divergieren.
Beispiel
\(\begin{aligned} \displaystyle\int_0^\infty e^{-x}\,dx&=\lim \limits_{b \to\infty}\big[-e^{-x}\big]_0^b\\ \\ &=\lim \limits_{b \to\infty}\big(-e^{-b}-(-e^{0})\big)\\ \\ &=\underbrace{\lim \limits_{b \to\infty}\big(-e^{-b}\big)}_{\rightarrow\,0}+1=1 \end{aligned}\)
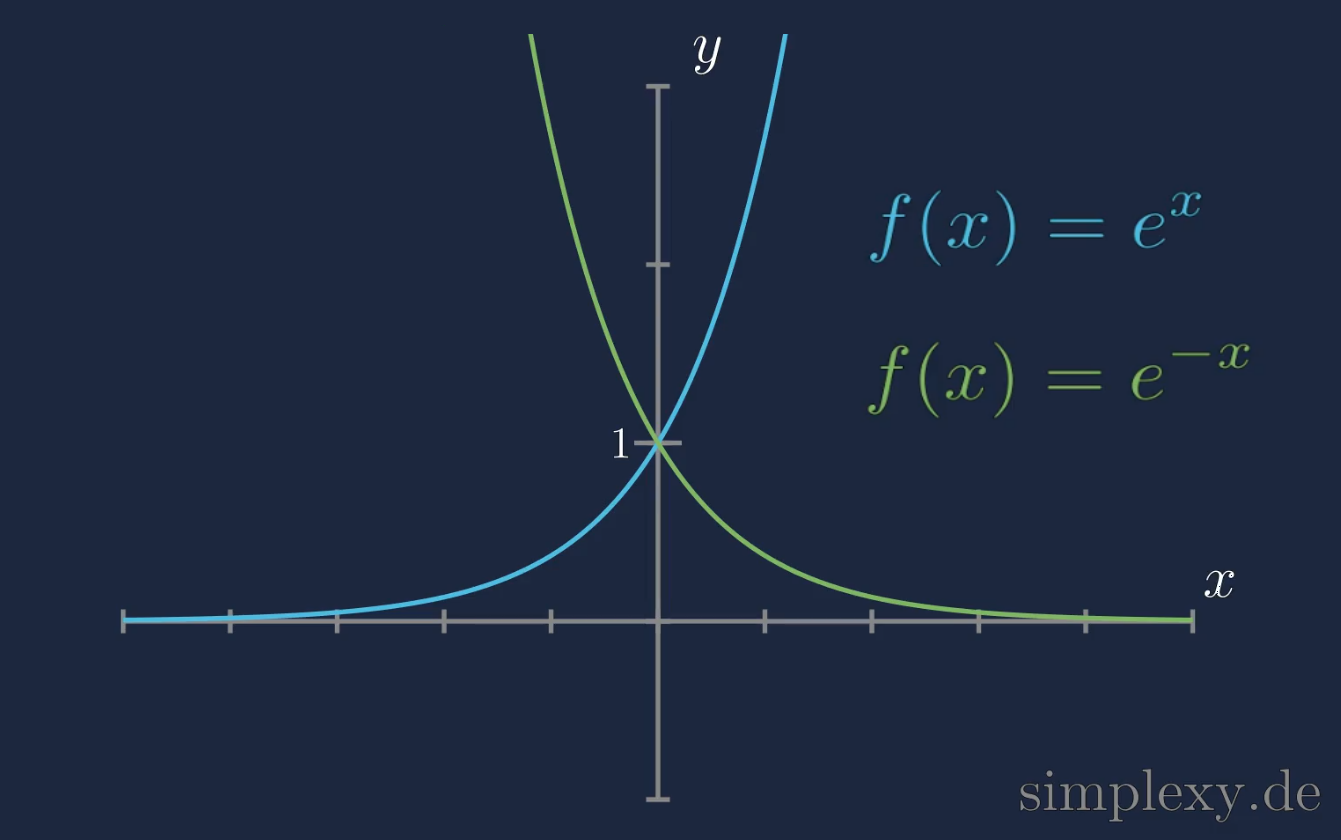
Wir sehen das die Funktion \(e^x\) gegen Unendlich divergiert für \(x \rightarrow \infty\). Im Falle der Funktion \(e^{-x}\) konvergiert die Funktion für \(x \rightarrow \infty\) gegen Null, daher konvergiert das uneigentliche Integal der Funktion \(e^{-x}\) im Intervall von \([0,\infty]\).
